表紙に戻る
四平方の定理
「およそ数学などというものは役に立たないもので、私などは初等数学の三平方の定理
すら日常生活で使ったことはなく、使うのはせいぜい、直角三角形の斜辺は他の二辺
よりも長いという事ぐらいだ」と豪語したのは、確か二葉亭四迷だと記憶しています。
正鵠を射たご意見ですが、このページでご紹介するのは、
その“役に立たない”三平方の定理を、更に拡張した定理についてです。
したがって“もっと役に立たない”定理かもしれません。(笑)
ちなみに二葉亭四迷というペンネームは、父親から
「小説家になるぐらいなら、くたばって死んじめぇ」
と言われたところから付けたそうです。→フタバッティシメイ
なんてウィットのある文人でしょうか!
この定理を思い付いた瞬間は今でも鮮明に覚えています。
それは大学受験の年の夏のことでした。
私は汗を流しながら数学の入試問題集に向かっていました。
そのとき、以下のような問題に出会ったのです。
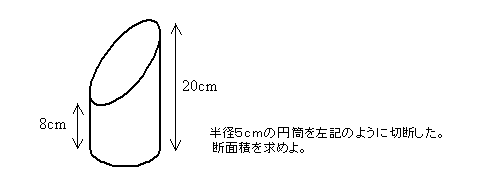 問題に使用されている具体的な数値は定かではありませんが、出題イメージは
正しいはずです。確か出題元は東京大学だったと記憶しております。
この問題の一般的な解法は、楕円の面積を求める公式を素直に利用する方法です。
楕円の面積は次のようにして求めます。
問題に使用されている具体的な数値は定かではありませんが、出題イメージは
正しいはずです。確か出題元は東京大学だったと記憶しております。
この問題の一般的な解法は、楕円の面積を求める公式を素直に利用する方法です。
楕円の面積は次のようにして求めます。
 さて、この公式を利用して、上記の問題を解いてみましょう。
断面の楕円の短半径は円筒の半径と等しいことは自明です。
さて、この公式を利用して、上記の問題を解いてみましょう。
断面の楕円の短半径は円筒の半径と等しいことは自明です。
 長半径の方は、切断する寸法差と円筒直径を直角三角形の直交する
二辺と捉え、三平方の定理で斜辺を求めることにより算出できます。
長半径の方は、切断する寸法差と円筒直径を直角三角形の直交する
二辺と捉え、三平方の定理で斜辺を求めることにより算出できます。
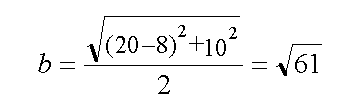 したがって、これらの長短の半径を楕円の面積公式に代入すれば、
したがって、これらの長短の半径を楕円の面積公式に代入すれば、
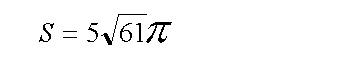 という答えを得られます。
このように、長半径算出のための立体的な把握が確立すれば、この問題はそれほど
難解なものではありません。しかし私はこの問題を見た瞬間、この素直な解法を思
い付くよりも先に、強烈なインスピレーションに襲われました。
仮説としての「四平方の定理」が脳裏の中に鮮明にイメージされたのです。
その仮説が正しいかどうか、まずはこの問題を例にして検証してみようと考え、
興奮で震える手を押さえながら筆算を始めたのです。
もう受験勉強どころではありませんでした。
さて、四平方の定理がどういうものかをご紹介いたします。
しかしその前に、通称ピタゴラスの定理と呼ばれている「三平方の定理」の復習から
始めましょう。この定理は、直角三角形の三辺において以下の図のような関係が成り
立つことを示しています。
という答えを得られます。
このように、長半径算出のための立体的な把握が確立すれば、この問題はそれほど
難解なものではありません。しかし私はこの問題を見た瞬間、この素直な解法を思
い付くよりも先に、強烈なインスピレーションに襲われました。
仮説としての「四平方の定理」が脳裏の中に鮮明にイメージされたのです。
その仮説が正しいかどうか、まずはこの問題を例にして検証してみようと考え、
興奮で震える手を押さえながら筆算を始めたのです。
もう受験勉強どころではありませんでした。
さて、四平方の定理がどういうものかをご紹介いたします。
しかしその前に、通称ピタゴラスの定理と呼ばれている「三平方の定理」の復習から
始めましょう。この定理は、直角三角形の三辺において以下の図のような関係が成り
立つことを示しています。
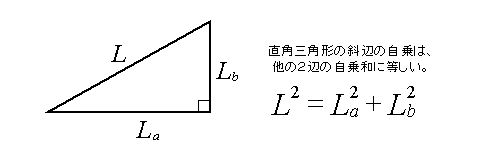 この定理は直角三角形という幾何図形における辺の相関を表現しています。
しかし、私はこの定理が幾何図形の寸法関係表現に留まらないと直感しました。
以下のように「長さを測定する定理」と捉え直すことが出来ると考えたのです。
この定理は直角三角形という幾何図形における辺の相関を表現しています。
しかし、私はこの定理が幾何図形の寸法関係表現に留まらないと直感しました。
以下のように「長さを測定する定理」と捉え直すことが出来ると考えたのです。
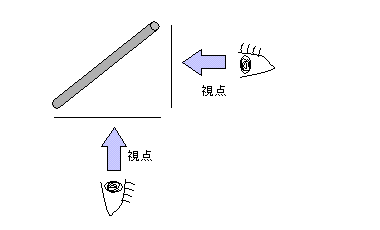 浮遊する棒の長さを測定するには、同一平面内の直交する2方向から
その棒の長さを測定し、それぞれの長さの自乗を合算して、その自乗根を得ればよい。
直交する2方向は、どのような組み合わせでも良いわけで、ちょうど棒が点に
なって見える方向を片方の観測方向に取れば、もう片方は棒の長さをそのまま
観察する事にもなります。
浮遊する棒の長さを測定するには、同一平面内の直交する2方向から
その棒の長さを測定し、それぞれの長さの自乗を合算して、その自乗根を得ればよい。
直交する2方向は、どのような組み合わせでも良いわけで、ちょうど棒が点に
なって見える方向を片方の観測方向に取れば、もう片方は棒の長さをそのまま
観察する事にもなります。
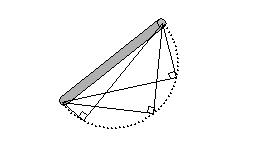 このように「三平方の定理」を「長さを測定する定理」として捉え直すことで、
「四平方の定理」がイメージし易くなります。その定理は以下の如くです。
このように「三平方の定理」を「長さを測定する定理」として捉え直すことで、
「四平方の定理」がイメージし易くなります。その定理は以下の如くです。
浮遊する板の面積を測定するには、直交する3方向からその板の面積を測定し、
それぞれの面積の自乗を合算し、その自乗根を得ればよい。
|
 これが、四平方の定理です。
浮遊する板は、平面でありさえすればその形状は任意です。
輪郭が曲線であっても構いません。
式で書くと以下のように表せます。
これが、四平方の定理です。
浮遊する板は、平面でありさえすればその形状は任意です。
輪郭が曲線であっても構いません。
式で書くと以下のように表せます。
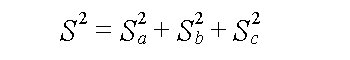 以上です。
最後に、この四平方の定理を検証するために震える手で私が行った検証の筆算を
記載しておきましょう。
問題の円筒を真上から見ると、それは半径5の真円として観察でき、その面積は、
以上です。
最後に、この四平方の定理を検証するために震える手で私が行った検証の筆算を
記載しておきましょう。
問題の円筒を真上から見ると、それは半径5の真円として観察でき、その面積は、
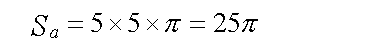 となる。
次に、楕円の切口を真正面に見るように観察すると、その楕円の長短の半径は
それぞれ、5および6となる。従って、この楕円の面積は、
となる。
次に、楕円の切口を真正面に見るように観察すると、その楕円の長短の半径は
それぞれ、5および6となる。従って、この楕円の面積は、
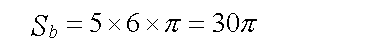 さらに、上記2方向と直行する方向から問題の円筒を観察すると、切口を真横
から見ることになり、その時の面積は
さらに、上記2方向と直行する方向から問題の円筒を観察すると、切口を真横
から見ることになり、その時の面積は
 である。
よって、これらを四平方の定理に代入すると以下のように断面積が求まる。
である。
よって、これらを四平方の定理に代入すると以下のように断面積が求まる。
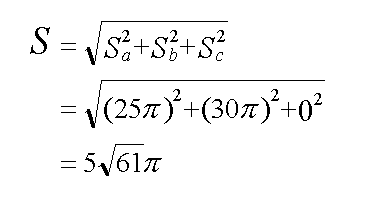 見事に一般的な解法と一致しました。
しかし、この四平方の定理を利用した解法は、どうみても最初に紹介した一般的な
解法より面倒な手続きとなっています。大学に合格するためには、あまり有効な公式
ではなさそうです。しかも、既に何百年も前から公知の事実かもしれません。
けれども、これを発見した時、私にとってはまさにヘウレーカと叫びたくなる瞬間
でした。私は誰に教わることなくこの美しい関係を発見したのは事実なのです。
翌日、早速私はこの発見を高校の数学教師に見てもらいました。
先生は「実に面白い。だが証明はできるのかな」と仰有いました。
実は、私は証明問題が大の苦手です。未だに精緻な証明が出来ずにいます。
数学の得意な方なら、余弦定理の拡張などで簡単に証明できる
かもしれません。その時、はじめて数学的な定理となるのでしょう。
しかし、射影方向による測定値から実体の値を算出するという描像に
自分の思索で到達できたという達成感は、決して消えることはありません。
見事に一般的な解法と一致しました。
しかし、この四平方の定理を利用した解法は、どうみても最初に紹介した一般的な
解法より面倒な手続きとなっています。大学に合格するためには、あまり有効な公式
ではなさそうです。しかも、既に何百年も前から公知の事実かもしれません。
けれども、これを発見した時、私にとってはまさにヘウレーカと叫びたくなる瞬間
でした。私は誰に教わることなくこの美しい関係を発見したのは事実なのです。
翌日、早速私はこの発見を高校の数学教師に見てもらいました。
先生は「実に面白い。だが証明はできるのかな」と仰有いました。
実は、私は証明問題が大の苦手です。未だに精緻な証明が出来ずにいます。
数学の得意な方なら、余弦定理の拡張などで簡単に証明できる
かもしれません。その時、はじめて数学的な定理となるのでしょう。
しかし、射影方向による測定値から実体の値を算出するという描像に
自分の思索で到達できたという達成感は、決して消えることはありません。
本ページ公開後、早速掲示板にてお二人の方から証明を頂きました。
この場を借りてお礼申上げると共に、記帳していただいた証明文を
掲載させていただきます。ありがとうございました。
表紙に戻る
 問題に使用されている具体的な数値は定かではありませんが、出題イメージは
正しいはずです。確か出題元は東京大学だったと記憶しております。
この問題の一般的な解法は、楕円の面積を求める公式を素直に利用する方法です。
楕円の面積は次のようにして求めます。
問題に使用されている具体的な数値は定かではありませんが、出題イメージは
正しいはずです。確か出題元は東京大学だったと記憶しております。
この問題の一般的な解法は、楕円の面積を求める公式を素直に利用する方法です。
楕円の面積は次のようにして求めます。
 さて、この公式を利用して、上記の問題を解いてみましょう。
断面の楕円の短半径は円筒の半径と等しいことは自明です。
さて、この公式を利用して、上記の問題を解いてみましょう。
断面の楕円の短半径は円筒の半径と等しいことは自明です。
 長半径の方は、切断する寸法差と円筒直径を直角三角形の直交する
二辺と捉え、三平方の定理で斜辺を求めることにより算出できます。
長半径の方は、切断する寸法差と円筒直径を直角三角形の直交する
二辺と捉え、三平方の定理で斜辺を求めることにより算出できます。
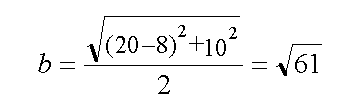 したがって、これらの長短の半径を楕円の面積公式に代入すれば、
したがって、これらの長短の半径を楕円の面積公式に代入すれば、
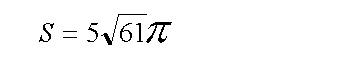 という答えを得られます。
このように、長半径算出のための立体的な把握が確立すれば、この問題はそれほど
難解なものではありません。しかし私はこの問題を見た瞬間、この素直な解法を思
い付くよりも先に、強烈なインスピレーションに襲われました。
仮説としての「四平方の定理」が脳裏の中に鮮明にイメージされたのです。
その仮説が正しいかどうか、まずはこの問題を例にして検証してみようと考え、
興奮で震える手を押さえながら筆算を始めたのです。
もう受験勉強どころではありませんでした。
さて、四平方の定理がどういうものかをご紹介いたします。
しかしその前に、通称ピタゴラスの定理と呼ばれている「三平方の定理」の復習から
始めましょう。この定理は、直角三角形の三辺において以下の図のような関係が成り
立つことを示しています。
という答えを得られます。
このように、長半径算出のための立体的な把握が確立すれば、この問題はそれほど
難解なものではありません。しかし私はこの問題を見た瞬間、この素直な解法を思
い付くよりも先に、強烈なインスピレーションに襲われました。
仮説としての「四平方の定理」が脳裏の中に鮮明にイメージされたのです。
その仮説が正しいかどうか、まずはこの問題を例にして検証してみようと考え、
興奮で震える手を押さえながら筆算を始めたのです。
もう受験勉強どころではありませんでした。
さて、四平方の定理がどういうものかをご紹介いたします。
しかしその前に、通称ピタゴラスの定理と呼ばれている「三平方の定理」の復習から
始めましょう。この定理は、直角三角形の三辺において以下の図のような関係が成り
立つことを示しています。
 この定理は直角三角形という幾何図形における辺の相関を表現しています。
しかし、私はこの定理が幾何図形の寸法関係表現に留まらないと直感しました。
以下のように「長さを測定する定理」と捉え直すことが出来ると考えたのです。
この定理は直角三角形という幾何図形における辺の相関を表現しています。
しかし、私はこの定理が幾何図形の寸法関係表現に留まらないと直感しました。
以下のように「長さを測定する定理」と捉え直すことが出来ると考えたのです。
 浮遊する棒の長さを測定するには、同一平面内の直交する2方向から
その棒の長さを測定し、それぞれの長さの自乗を合算して、その自乗根を得ればよい。
直交する2方向は、どのような組み合わせでも良いわけで、ちょうど棒が点に
なって見える方向を片方の観測方向に取れば、もう片方は棒の長さをそのまま
観察する事にもなります。
浮遊する棒の長さを測定するには、同一平面内の直交する2方向から
その棒の長さを測定し、それぞれの長さの自乗を合算して、その自乗根を得ればよい。
直交する2方向は、どのような組み合わせでも良いわけで、ちょうど棒が点に
なって見える方向を片方の観測方向に取れば、もう片方は棒の長さをそのまま
観察する事にもなります。
 このように「三平方の定理」を「長さを測定する定理」として捉え直すことで、
「四平方の定理」がイメージし易くなります。その定理は以下の如くです。
このように「三平方の定理」を「長さを測定する定理」として捉え直すことで、
「四平方の定理」がイメージし易くなります。その定理は以下の如くです。
 これが、四平方の定理です。
浮遊する板は、平面でありさえすればその形状は任意です。
輪郭が曲線であっても構いません。
式で書くと以下のように表せます。
これが、四平方の定理です。
浮遊する板は、平面でありさえすればその形状は任意です。
輪郭が曲線であっても構いません。
式で書くと以下のように表せます。
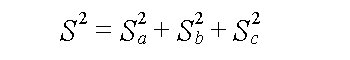 以上です。
最後に、この四平方の定理を検証するために震える手で私が行った検証の筆算を
記載しておきましょう。
問題の円筒を真上から見ると、それは半径5の真円として観察でき、その面積は、
以上です。
最後に、この四平方の定理を検証するために震える手で私が行った検証の筆算を
記載しておきましょう。
問題の円筒を真上から見ると、それは半径5の真円として観察でき、その面積は、
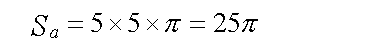 となる。
次に、楕円の切口を真正面に見るように観察すると、その楕円の長短の半径は
それぞれ、5および6となる。従って、この楕円の面積は、
となる。
次に、楕円の切口を真正面に見るように観察すると、その楕円の長短の半径は
それぞれ、5および6となる。従って、この楕円の面積は、
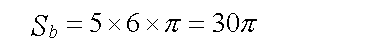 さらに、上記2方向と直行する方向から問題の円筒を観察すると、切口を真横
から見ることになり、その時の面積は
さらに、上記2方向と直行する方向から問題の円筒を観察すると、切口を真横
から見ることになり、その時の面積は
 である。
よって、これらを四平方の定理に代入すると以下のように断面積が求まる。
である。
よって、これらを四平方の定理に代入すると以下のように断面積が求まる。
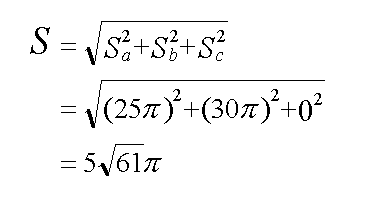 見事に一般的な解法と一致しました。
しかし、この四平方の定理を利用した解法は、どうみても最初に紹介した一般的な
解法より面倒な手続きとなっています。大学に合格するためには、あまり有効な公式
ではなさそうです。しかも、既に何百年も前から公知の事実かもしれません。
けれども、これを発見した時、私にとってはまさにヘウレーカと叫びたくなる瞬間
でした。私は誰に教わることなくこの美しい関係を発見したのは事実なのです。
翌日、早速私はこの発見を高校の数学教師に見てもらいました。
先生は「実に面白い。だが証明はできるのかな」と仰有いました。
実は、私は証明問題が大の苦手です。未だに精緻な証明が出来ずにいます。
数学の得意な方なら、余弦定理の拡張などで簡単に証明できる
かもしれません。その時、はじめて数学的な定理となるのでしょう。
しかし、射影方向による測定値から実体の値を算出するという描像に
自分の思索で到達できたという達成感は、決して消えることはありません。
見事に一般的な解法と一致しました。
しかし、この四平方の定理を利用した解法は、どうみても最初に紹介した一般的な
解法より面倒な手続きとなっています。大学に合格するためには、あまり有効な公式
ではなさそうです。しかも、既に何百年も前から公知の事実かもしれません。
けれども、これを発見した時、私にとってはまさにヘウレーカと叫びたくなる瞬間
でした。私は誰に教わることなくこの美しい関係を発見したのは事実なのです。
翌日、早速私はこの発見を高校の数学教師に見てもらいました。
先生は「実に面白い。だが証明はできるのかな」と仰有いました。
実は、私は証明問題が大の苦手です。未だに精緻な証明が出来ずにいます。
数学の得意な方なら、余弦定理の拡張などで簡単に証明できる
かもしれません。その時、はじめて数学的な定理となるのでしょう。
しかし、射影方向による測定値から実体の値を算出するという描像に
自分の思索で到達できたという達成感は、決して消えることはありません。