(注)これは単なる挿絵です
本文内容とは関係ありません
学校で「パスカルの三角形」を教わった私は、その規則性に興味を持ち、
“三項”の場合には、どんな法則が存在するのかという好奇心にかられました。
とにかく、やってみればいいことです。
紙と鉛筆と根気さえあれば誰にでもできる作業です。
私は早速、展開作業を開始しました。
(a+b+c)1 = a + b + c
(a+b+c)2 =
a2 +
b2 +
c2 +
2ab +
2bc +
2ca
(a+b+c)3 =
a3 +
b3 +
c3 +
3a2b +
3b2c +
3c2a +
3ab2 +
3bc2 +
3ca2 + 6abc
(a+b+c)4 =
a4 +
b4 +
c4 +
4a3b +
4b3c +
4c3a +
4ab3 +
4bc3 +
4ca3 +
6a2b2 +
6b2c2 +
6c2a2 +
6a2b2 +
12a3bc +
12b3ca +
12c3ab
(a+b+c)5 =
a5 +
b5 +
c5 +
5a4b +
5b4c +
5c4a +
5ab4 +
5bc4 +
5ca4 +
10a3b2 +
10b3c2 +
10c3a2 +
10a2b3 +
10b2c3 +
10c2a3 +
20a3bc +
20b3ca +
20c3ab +
30a2b2c +
30b2c2a +
30c2a2b
これらの結果を眺めて、私はすぐにこの展開係数の中に
「3つのパスカルの三角形」が含まれていることに気づきました。
そして早速、以下のような三角錐を描いてみたのです。
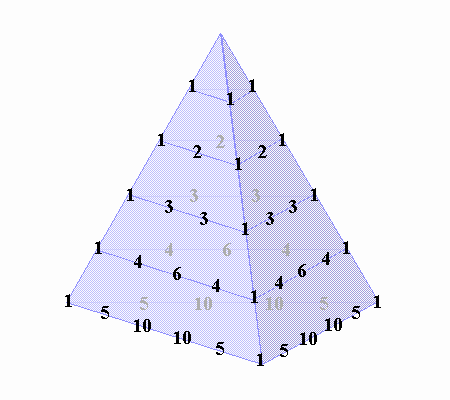 しかし残念なことに、このアイディアは完全ではありませんでした。
この三角錐では記載しきれない係数が存在するのです。
それは次数が上がるほど増えていきました。
しかし残念なことに、このアイディアは完全ではありませんでした。
この三角錐では記載しきれない係数が存在するのです。
それは次数が上がるほど増えていきました。
3乗 →
6abc
4乗 →
12a3bc +
12b3ca +
12c3ab
5乗 →
20a3bc +
20b3ca +
20c3ab +
30a2b2c +
30b2c2a +
30c2a2b
やっぱり、この思い付きは失敗だったのでしょうか。
私は多少くじけそうになりました。
しかし、この三角錐のアイディアは、破棄するにはもったいない気がしました。
確かに表現しきれない係数がありますが、もう一押しで真理に到達する気配がしたのです。
「どうにかして完全な描象を得たい」
私は何週間もいろいろな図形を書き散らしました。
そして、ある日ついに閃きました。
三角形が「平面」なら、三角錐は「立体」です。
私は今まで三角錐の表面にのみ着目していました。
しかし「立体」は、その内部に構造を持っているのです。
表現できない係数項は、実は三角錐の内部に配置されるのではないか?
これが、私の閃きでした。
そして、問題の係数が見事な均整をもって納まるのを確認したのです。
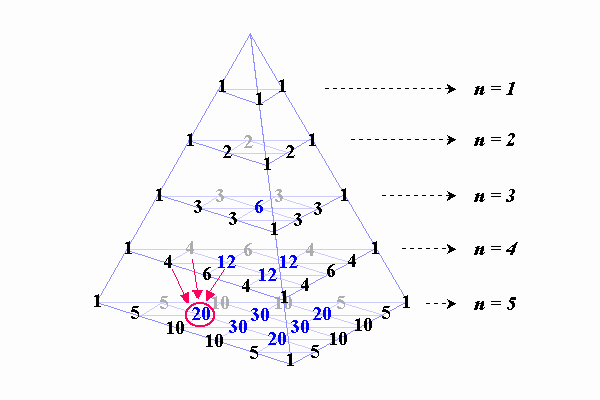 この美しい三角錐を描ききった時の感動を忘れません。
私はパスカルの三角形を拡張することができたのです!
この三角錐に粋な名前を与えようと思ったのですが、なかなか考えつかず、
しかたなく自分の名前を取って渋々「カトウの三角錐」と呼んでいます。(笑)
この「カトウの三角錐」には、「パスカルの三角形」と同様な規則性が
あることもすぐに確認できました。
「ある数は、その1つ上の行の隣接する3つの数の和によって求まる」
例えば、上図の赤で示された部分では、4+4+12=20 という関係が成り立っています。
この規則性を数式で確認するため、私は「三項定理」を組み立てることにしました。
そのためには、まず組み合わせ演算子を拡張する必要がありました。
以下が私が勝手に発案した「Combinationの拡張表現」です。
この美しい三角錐を描ききった時の感動を忘れません。
私はパスカルの三角形を拡張することができたのです!
この三角錐に粋な名前を与えようと思ったのですが、なかなか考えつかず、
しかたなく自分の名前を取って渋々「カトウの三角錐」と呼んでいます。(笑)
この「カトウの三角錐」には、「パスカルの三角形」と同様な規則性が
あることもすぐに確認できました。
「ある数は、その1つ上の行の隣接する3つの数の和によって求まる」
例えば、上図の赤で示された部分では、4+4+12=20 という関係が成り立っています。
この規則性を数式で確認するため、私は「三項定理」を組み立てることにしました。
そのためには、まず組み合わせ演算子を拡張する必要がありました。
以下が私が勝手に発案した「Combinationの拡張表現」です。
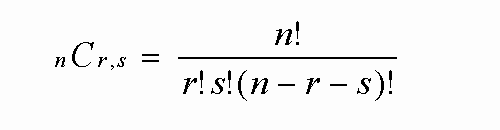 上記の「拡張されたConbination記述」を使えば、
「三項定理」として以下のような式を与えることができます。
上記の「拡張されたConbination記述」を使えば、
「三項定理」として以下のような式を与えることができます。
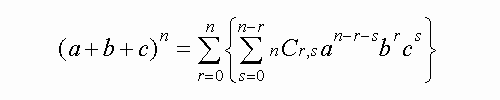 そして、三項定理における係数の漸化式は、以下のようになります。
そして、三項定理における係数の漸化式は、以下のようになります。
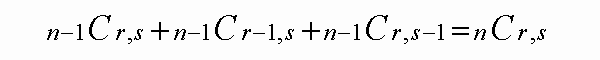 ここで、二項定理の時と同様な方法を使い左辺を展開整理してみます。
ここで、二項定理の時と同様な方法を使い左辺を展開整理してみます。
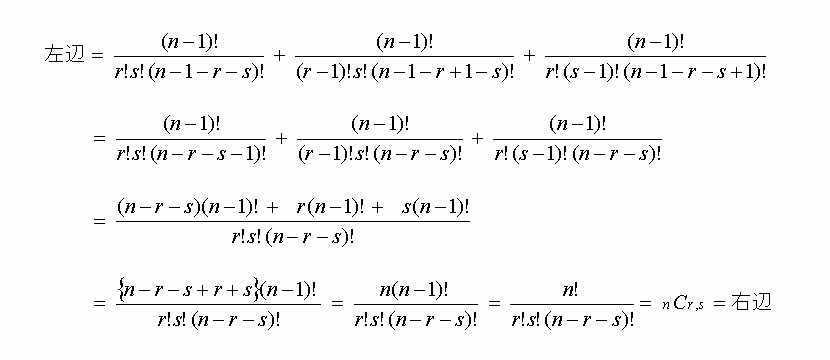 見事に、三項定理における漸化式の検証も成功しました。
「カトウの三角錐」は、その一つの断面の中にも美しい規則性があります。
断面の図形は正三角形になるわけですが、その3つの頂点がそれぞれ a,b,c の最高次数項を表します。
そして、それぞれの係数の位置における「頂点との距離」によって a,b,c の次数が決るのです。
例えば、n = 4 の断面を取出してみましょう。
見事に、三項定理における漸化式の検証も成功しました。
「カトウの三角錐」は、その一つの断面の中にも美しい規則性があります。
断面の図形は正三角形になるわけですが、その3つの頂点がそれぞれ a,b,c の最高次数項を表します。
そして、それぞれの係数の位置における「頂点との距離」によって a,b,c の次数が決るのです。
例えば、n = 4 の断面を取出してみましょう。
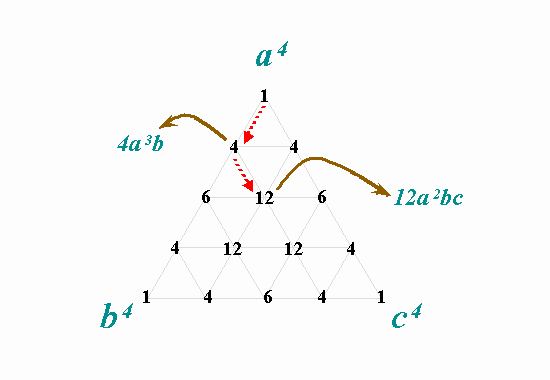 図の赤い点線矢印に注目して下さい。
a4 の頂点から出発して、頂点 a から1つ離れ、かつ頂点 b に1つ近づくと、a3b の項となります。
更に頂点 a から1つ離れ、今度は頂点 c に1つ近づくと a2bc の項になるわけです。
こうして「カトウの三角錐」は、見事に「パスカルの三角形」の拡張に成功しました。
この宝石の結晶のように美しい描像は、私を大変満足させました。
しかし二項定理を三項定理に拡張できるのなら、四項、五項と進めたくなるのが人情です。
そして、最後は「n項定理」という一般系にしてこそ、新しい領域の開拓であり、真の拡張と言えるでしょう。
でも、私は足を止めました。
三角形という「平面」の次に来るのが、三角錐という「立体」だとしたら、
その次に来るのは、どう考えても「超立体」つまり4次元物体です。
確かに、Combination拡張をn元化すれば、「数式」としての「n項定理」表現は可能でしょう。
それは容易に想像が付きます。しかし「パスカルの三角形」のような描像を与えることは出来ません。
そんなわけで、しばらく私はこの問題から離れていました。
「カトウの三角錐」という結論を得たことで、それなりの満足感を得たというのも事実でした。
しかしまたある日、突然と閃きが起りました。
それは、「カトウの三角錐」の断面を以下のように並べた瞬間でした。
図の赤い点線矢印に注目して下さい。
a4 の頂点から出発して、頂点 a から1つ離れ、かつ頂点 b に1つ近づくと、a3b の項となります。
更に頂点 a から1つ離れ、今度は頂点 c に1つ近づくと a2bc の項になるわけです。
こうして「カトウの三角錐」は、見事に「パスカルの三角形」の拡張に成功しました。
この宝石の結晶のように美しい描像は、私を大変満足させました。
しかし二項定理を三項定理に拡張できるのなら、四項、五項と進めたくなるのが人情です。
そして、最後は「n項定理」という一般系にしてこそ、新しい領域の開拓であり、真の拡張と言えるでしょう。
でも、私は足を止めました。
三角形という「平面」の次に来るのが、三角錐という「立体」だとしたら、
その次に来るのは、どう考えても「超立体」つまり4次元物体です。
確かに、Combination拡張をn元化すれば、「数式」としての「n項定理」表現は可能でしょう。
それは容易に想像が付きます。しかし「パスカルの三角形」のような描像を与えることは出来ません。
そんなわけで、しばらく私はこの問題から離れていました。
「カトウの三角錐」という結論を得たことで、それなりの満足感を得たというのも事実でした。
しかしまたある日、突然と閃きが起りました。
それは、「カトウの三角錐」の断面を以下のように並べた瞬間でした。
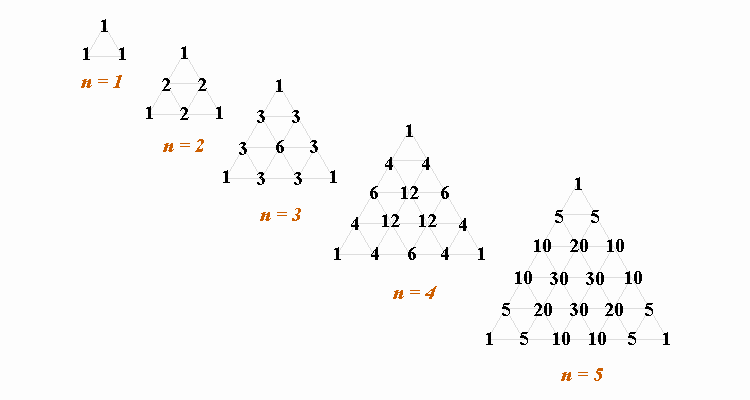 確かに「カトウの三角錐」は“立体”です。しかし、その断面は「正三角形」という“平面”です。
という事は、四項定理の“超立体”の断面形状は、“立体”として並べることが可能なのではないか?
これが私の閃きでした。そしてその立体は、必ずや「正四面体」であろうと直観しました。
早速、紙と鉛筆、そして今まで以上の“根気”を発動することにしました。
確かに「カトウの三角錐」は“立体”です。しかし、その断面は「正三角形」という“平面”です。
という事は、四項定理の“超立体”の断面形状は、“立体”として並べることが可能なのではないか?
これが私の閃きでした。そしてその立体は、必ずや「正四面体」であろうと直観しました。
早速、紙と鉛筆、そして今まで以上の“根気”を発動することにしました。
(a+b+c+d)1 = a + b + c + d
(a+b+c+d)2 =
a2 +
b2 +
c2 +
d2 +
2ab +
2bc +
2cd +
2da +
2ac +
2bd
(a+b+c+d)3 =
a3 +
b3 +
c3 +
d3 +
3a2b +
3b2c +
3c2d +
3d2a +
3a2c +
3b2d +
3ab2 +
3bc2 +
3cd2 +
3da2 +
3ac2 +
3bd2 +
6abc +
6bcd +
6cda +
6dab
(a+b+c+d)4 =
a4 +
b4 +
c4 +
d4 +
4a3b +
4b3c +
4c3d +
4d3a +
4a3c +
4b3d +
4ab3 +
4bc3 +
4cd3 +
4da3 +
4ac3 +
4bd3 +
6a2b2 +
6b2c2 +
6c2a2 +
6a2d2 +
6a2b2 +
6b2d2 +
12a2bc +
12ab2c +
12abc2 +
12a2bd +
12ab2d +
12abd2 +
12a2cd +
12ac2d +
12acd2 +
12b2cd +
12bc2d +
12bcd2 +
24abcd
さて、これら四項展開の係数を、結晶のように並べることが出来るでしょうか?
結果は大成功でした。以下のように見事な正四面体の隊列が姿を現したのです!
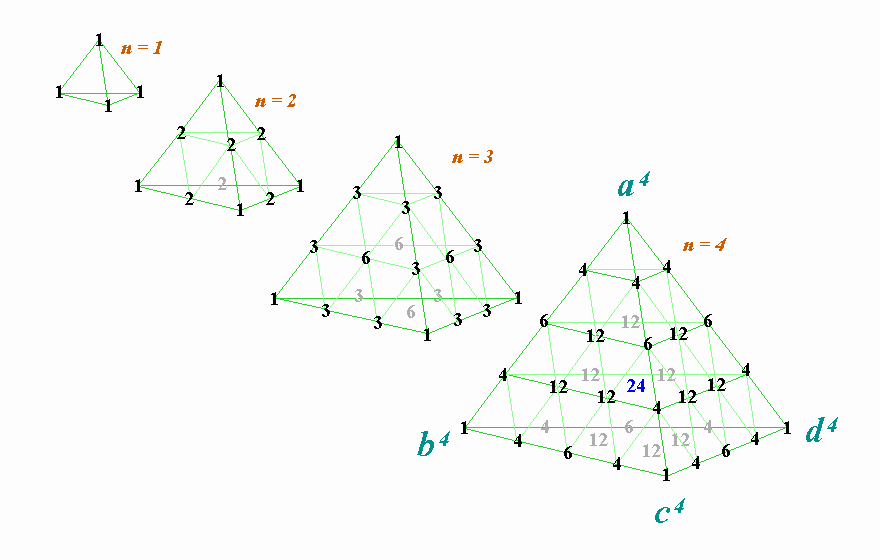 今度は、正四面体の4つの頂点がそれぞれ a,b,c,d の最高次数項を表します。
それぞれの係数位置に関する「頂点との距離」の関係も「カトウの三角錐」と同様に成立ちます。
もちろん、1つ前の次数における隣接する係数の和が、次の次数の係数となる規則性も存在します。
見事な美しさです!
けれども、私たち3次元空間で生きる人間に描ける描像はここまでです。
次は、断面形状でさえ「4次元物体」になってしまうからです。
しかし、自らの思索で描像の限界まで達することができたという満足感は、
夜空の星のように、いつまでも私の心の内で輝いているのです。
今度は、正四面体の4つの頂点がそれぞれ a,b,c,d の最高次数項を表します。
それぞれの係数位置に関する「頂点との距離」の関係も「カトウの三角錐」と同様に成立ちます。
もちろん、1つ前の次数における隣接する係数の和が、次の次数の係数となる規則性も存在します。
見事な美しさです!
けれども、私たち3次元空間で生きる人間に描ける描像はここまでです。
次は、断面形状でさえ「4次元物体」になってしまうからです。
しかし、自らの思索で描像の限界まで達することができたという満足感は、
夜空の星のように、いつまでも私の心の内で輝いているのです。
表紙に戻る
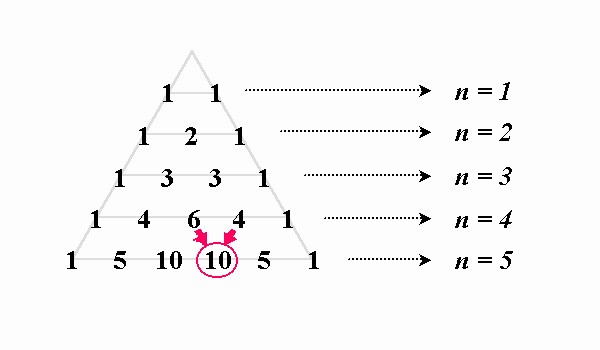 これが「パスカルの三角形」です。
この三角形に並べられた数字には、次のような法則があるのがわかります。
「ある数は、その1つ上の行の隣接する左右の数の和によって求まる」
例えば、上図の赤い部分では、6+4=10 となっています。
どうしてこんな規則性が存在するのでしょうか?
この二項式のn乗展開における係数は、
現代の数学では以下のような数式で表現されます。
これが「パスカルの三角形」です。
この三角形に並べられた数字には、次のような法則があるのがわかります。
「ある数は、その1つ上の行の隣接する左右の数の和によって求まる」
例えば、上図の赤い部分では、6+4=10 となっています。
どうしてこんな規則性が存在するのでしょうか?
この二項式のn乗展開における係数は、
現代の数学では以下のような数式で表現されます。
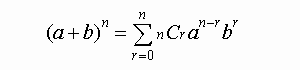 これは“二項定理”と呼ばれ、右辺の係数 nCr を“二項係数”と言います。
結局、パスカルが見出した“美”は、確率計算で多用される組合せ演算子(Combination)で
表現されます。事実パスカルは、ある賭博師から“賭けを中断した際の公平な配分方法”を
依頼され、その確率計算方法を検討している最中に「パスカルの三角形」を発見したそうです。
この二項係数で「パスカルの三角形」における規則性も簡単に証明できます。
6+4=10 の関係を二項係数を利用して表現すると、
以下のような一般的な漸化式になります。
これは“二項定理”と呼ばれ、右辺の係数 nCr を“二項係数”と言います。
結局、パスカルが見出した“美”は、確率計算で多用される組合せ演算子(Combination)で
表現されます。事実パスカルは、ある賭博師から“賭けを中断した際の公平な配分方法”を
依頼され、その確率計算方法を検討している最中に「パスカルの三角形」を発見したそうです。
この二項係数で「パスカルの三角形」における規則性も簡単に証明できます。
6+4=10 の関係を二項係数を利用して表現すると、
以下のような一般的な漸化式になります。
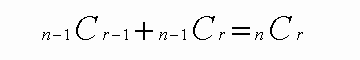 この漸化式が成立つかどうか、左辺の式を階乗表現にて展開整理して検証してみます。
左辺の第一項の分母分子に r を掛け、第二項の分母分子に (n-r) を掛けることで
通分が可能となり、更に整理を進めると右辺に等しくなることが示されます。
この漸化式が成立つかどうか、左辺の式を階乗表現にて展開整理して検証してみます。
左辺の第一項の分母分子に r を掛け、第二項の分母分子に (n-r) を掛けることで
通分が可能となり、更に整理を進めると右辺に等しくなることが示されます。
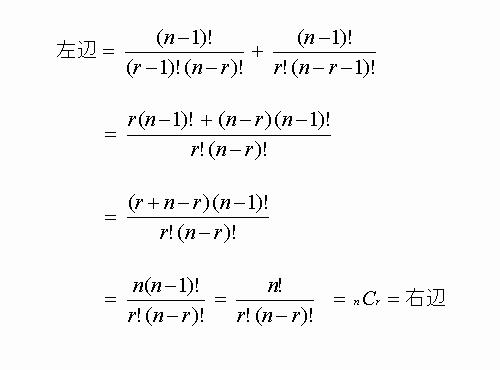 以上のように数式は幾何学的な“美の均整”を論理的に解明する力を持っています。
しかし人が“美”を感じるのは「解明の瞬間」より、むしろ「発見の瞬間」に
より強く宿るような気がしてなりません。それは、私自身の体験に基づく感覚です。
これからお話しするのは、私が高校の頃「パスカルの三角形」を拡張した経験談です。
以上のように数式は幾何学的な“美の均整”を論理的に解明する力を持っています。
しかし人が“美”を感じるのは「解明の瞬間」より、むしろ「発見の瞬間」に
より強く宿るような気がしてなりません。それは、私自身の体験に基づく感覚です。
これからお話しするのは、私が高校の頃「パスカルの三角形」を拡張した経験談です。

 しかし残念なことに、このアイディアは完全ではありませんでした。
この三角錐では記載しきれない係数が存在するのです。
それは次数が上がるほど増えていきました。
しかし残念なことに、このアイディアは完全ではありませんでした。
この三角錐では記載しきれない係数が存在するのです。
それは次数が上がるほど増えていきました。
 この美しい三角錐を描ききった時の感動を忘れません。
私はパスカルの三角形を拡張することができたのです!
この三角錐に粋な名前を与えようと思ったのですが、なかなか考えつかず、
しかたなく自分の名前を取って渋々「カトウの三角錐」と呼んでいます。(笑)
この「カトウの三角錐」には、「パスカルの三角形」と同様な規則性が
あることもすぐに確認できました。
「ある数は、その1つ上の行の隣接する3つの数の和によって求まる」
例えば、上図の赤で示された部分では、4+4+12=20 という関係が成り立っています。
この規則性を数式で確認するため、私は「三項定理」を組み立てることにしました。
そのためには、まず組み合わせ演算子を拡張する必要がありました。
以下が私が勝手に発案した「Combinationの拡張表現」です。
この美しい三角錐を描ききった時の感動を忘れません。
私はパスカルの三角形を拡張することができたのです!
この三角錐に粋な名前を与えようと思ったのですが、なかなか考えつかず、
しかたなく自分の名前を取って渋々「カトウの三角錐」と呼んでいます。(笑)
この「カトウの三角錐」には、「パスカルの三角形」と同様な規則性が
あることもすぐに確認できました。
「ある数は、その1つ上の行の隣接する3つの数の和によって求まる」
例えば、上図の赤で示された部分では、4+4+12=20 という関係が成り立っています。
この規則性を数式で確認するため、私は「三項定理」を組み立てることにしました。
そのためには、まず組み合わせ演算子を拡張する必要がありました。
以下が私が勝手に発案した「Combinationの拡張表現」です。
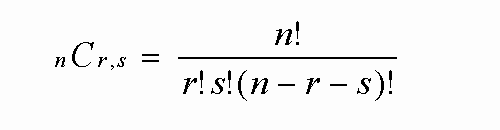 上記の「拡張されたConbination記述」を使えば、
「三項定理」として以下のような式を与えることができます。
上記の「拡張されたConbination記述」を使えば、
「三項定理」として以下のような式を与えることができます。
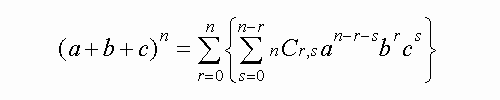 そして、三項定理における係数の漸化式は、以下のようになります。
そして、三項定理における係数の漸化式は、以下のようになります。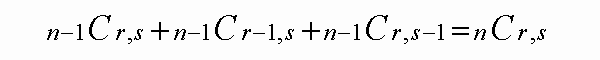 ここで、二項定理の時と同様な方法を使い左辺を展開整理してみます。
ここで、二項定理の時と同様な方法を使い左辺を展開整理してみます。
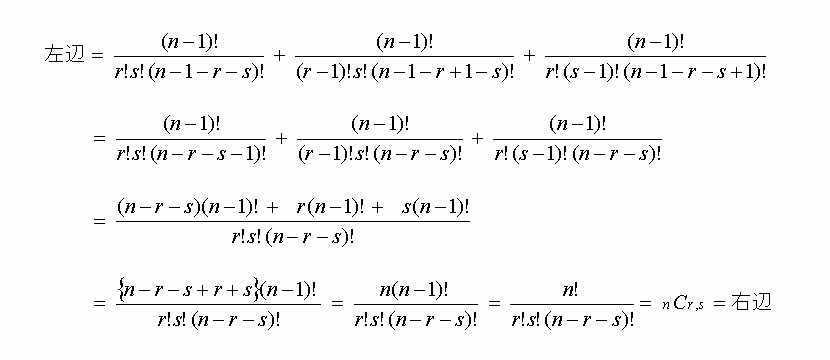 見事に、三項定理における漸化式の検証も成功しました。
「カトウの三角錐」は、その一つの断面の中にも美しい規則性があります。
断面の図形は正三角形になるわけですが、その3つの頂点がそれぞれ a,b,c の最高次数項を表します。
そして、それぞれの係数の位置における「頂点との距離」によって a,b,c の次数が決るのです。
例えば、n = 4 の断面を取出してみましょう。
見事に、三項定理における漸化式の検証も成功しました。
「カトウの三角錐」は、その一つの断面の中にも美しい規則性があります。
断面の図形は正三角形になるわけですが、その3つの頂点がそれぞれ a,b,c の最高次数項を表します。
そして、それぞれの係数の位置における「頂点との距離」によって a,b,c の次数が決るのです。
例えば、n = 4 の断面を取出してみましょう。
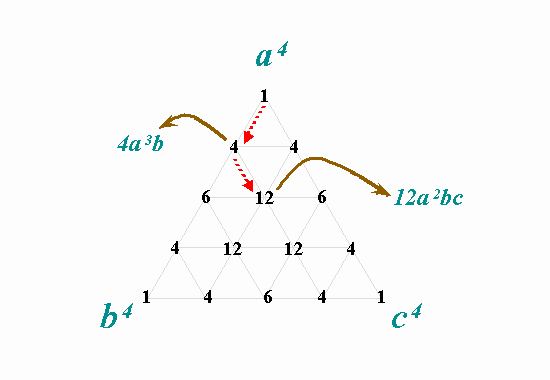 図の赤い点線矢印に注目して下さい。
a4 の頂点から出発して、頂点 a から1つ離れ、かつ頂点 b に1つ近づくと、a3b の項となります。
更に頂点 a から1つ離れ、今度は頂点 c に1つ近づくと a2bc の項になるわけです。
こうして「カトウの三角錐」は、見事に「パスカルの三角形」の拡張に成功しました。
この宝石の結晶のように美しい描像は、私を大変満足させました。
しかし二項定理を三項定理に拡張できるのなら、四項、五項と進めたくなるのが人情です。
そして、最後は「n項定理」という一般系にしてこそ、新しい領域の開拓であり、真の拡張と言えるでしょう。
でも、私は足を止めました。
三角形という「平面」の次に来るのが、三角錐という「立体」だとしたら、
その次に来るのは、どう考えても「超立体」つまり4次元物体です。
確かに、Combination拡張をn元化すれば、「数式」としての「n項定理」表現は可能でしょう。
それは容易に想像が付きます。しかし「パスカルの三角形」のような描像を与えることは出来ません。
そんなわけで、しばらく私はこの問題から離れていました。
「カトウの三角錐」という結論を得たことで、それなりの満足感を得たというのも事実でした。
しかしまたある日、突然と閃きが起りました。
それは、「カトウの三角錐」の断面を以下のように並べた瞬間でした。
図の赤い点線矢印に注目して下さい。
a4 の頂点から出発して、頂点 a から1つ離れ、かつ頂点 b に1つ近づくと、a3b の項となります。
更に頂点 a から1つ離れ、今度は頂点 c に1つ近づくと a2bc の項になるわけです。
こうして「カトウの三角錐」は、見事に「パスカルの三角形」の拡張に成功しました。
この宝石の結晶のように美しい描像は、私を大変満足させました。
しかし二項定理を三項定理に拡張できるのなら、四項、五項と進めたくなるのが人情です。
そして、最後は「n項定理」という一般系にしてこそ、新しい領域の開拓であり、真の拡張と言えるでしょう。
でも、私は足を止めました。
三角形という「平面」の次に来るのが、三角錐という「立体」だとしたら、
その次に来るのは、どう考えても「超立体」つまり4次元物体です。
確かに、Combination拡張をn元化すれば、「数式」としての「n項定理」表現は可能でしょう。
それは容易に想像が付きます。しかし「パスカルの三角形」のような描像を与えることは出来ません。
そんなわけで、しばらく私はこの問題から離れていました。
「カトウの三角錐」という結論を得たことで、それなりの満足感を得たというのも事実でした。
しかしまたある日、突然と閃きが起りました。
それは、「カトウの三角錐」の断面を以下のように並べた瞬間でした。
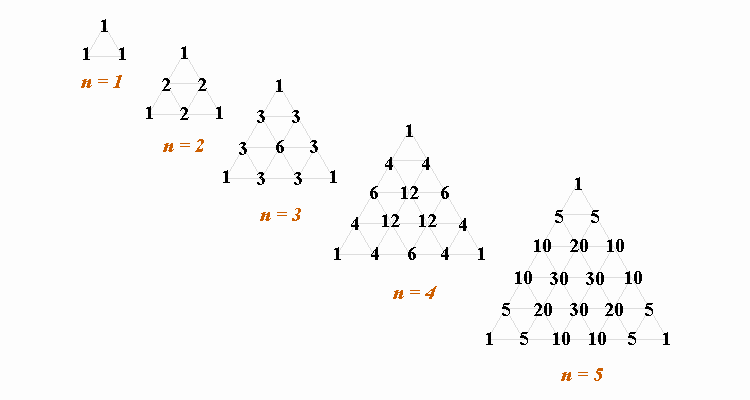 確かに「カトウの三角錐」は“立体”です。しかし、その断面は「正三角形」という“平面”です。
という事は、四項定理の“超立体”の断面形状は、“立体”として並べることが可能なのではないか?
これが私の閃きでした。そしてその立体は、必ずや「正四面体」であろうと直観しました。
早速、紙と鉛筆、そして今まで以上の“根気”を発動することにしました。
確かに「カトウの三角錐」は“立体”です。しかし、その断面は「正三角形」という“平面”です。
という事は、四項定理の“超立体”の断面形状は、“立体”として並べることが可能なのではないか?
これが私の閃きでした。そしてその立体は、必ずや「正四面体」であろうと直観しました。
早速、紙と鉛筆、そして今まで以上の“根気”を発動することにしました。
 今度は、正四面体の4つの頂点がそれぞれ a,b,c,d の最高次数項を表します。
それぞれの係数位置に関する「頂点との距離」の関係も「カトウの三角錐」と同様に成立ちます。
もちろん、1つ前の次数における隣接する係数の和が、次の次数の係数となる規則性も存在します。
見事な美しさです!
けれども、私たち3次元空間で生きる人間に描ける描像はここまでです。
次は、断面形状でさえ「4次元物体」になってしまうからです。
しかし、自らの思索で描像の限界まで達することができたという満足感は、
夜空の星のように、いつまでも私の心の内で輝いているのです。
今度は、正四面体の4つの頂点がそれぞれ a,b,c,d の最高次数項を表します。
それぞれの係数位置に関する「頂点との距離」の関係も「カトウの三角錐」と同様に成立ちます。
もちろん、1つ前の次数における隣接する係数の和が、次の次数の係数となる規則性も存在します。
見事な美しさです!
けれども、私たち3次元空間で生きる人間に描ける描像はここまでです。
次は、断面形状でさえ「4次元物体」になってしまうからです。
しかし、自らの思索で描像の限界まで達することができたという満足感は、
夜空の星のように、いつまでも私の心の内で輝いているのです。