特殊相対性理論の一考察

特殊相対性理論の一考察
加藤一郎
kato@c3-net.ne.jp

要約

　　特殊相対性理論における「光速度不変の原理」の仮定に対し、光の速度が光源に対して一定であるとするリッツの「一定射出速度の仮説」の再考を試みる。光を古典的な波動としてではなく、量子としてとらえ直すことでこの仮説を検証する。また、マックスウェルの電磁波の波動方程式の基準座標が、すべての慣性系を対象としているという従来の見解に関して、ローレンツ力の定義から再考し直し、それが電磁波の発生源の座標系を基準としていることを示す。最後に本稿の主張を検出する方法について議論し、特殊相対性理論を検証する新しい思考実験として“周回衛星のパラックス”を提示する。また、補足にて“"時間”に関する考察も添えた。

１．特殊相対性理論の仮定

　　特殊相対性理論は、二つの要請から理論を展開する。すなわち、

①あらゆる自然法則は互いに相対的に一様に動いているすべての座標系において同一の形をもつ。(ガリレイの相対性原理)

②光は常に真空中を一定の速さｃで伝播し、この速さは光源の運動状態には無関係である。(光速度不変の原理)

　この二つの要請を仮定すると、特殊相対性理論の数学的展開とその帰結である現象の予測(同時刻の相対性、時空に対するローレンツ変換、質量とエネルギーの等価性など）は論理的に矛盾が無く、しかも完結していることは明らかである。しかし、要請①に対して要請②が強い絶対性を主張した仮定であることは否めない。アインシュタインが特殊相対性理論を展開した当時の物理学者にとって、物理現象は粒子的なものと波動的なものに二分され、光は後者であることが衆目の一致するところであった。波動的なものならそれを生じさせる媒質が存在するはずであるという推論から“エーテル”が仮定され、それに対する地球の相対運動を発見しようという試みがなされた。それが失敗に終わり、ローレンツはエーテルの存在を前提にしたまま、時空に対して変換(ローレンツ変換)を施すことでその実験事実を説明することを提唱した。一方、アインシュタインはエーテルの存在を否定し、 ②の要請である“光速度不変”の仮定から出発することでこの現象を説明しようとし、特殊相対性理論を展開した。
　このように特殊相対性理論は、光→波動→媒質→エーテルという物理現象説明の過程の中で、ガリレイの相対性原理を満たすべくエーテル(絶対静止空間)を否定し、最後に光速度不変の原理、すなわち絶対速度ｃを要請して生まれたと言える。本稿は、アインシュタインと同様絶対静止空間を否定し、ガリレイの相対性原理を要請する（要請①の維持）。しかし、光速度不変の原理は持ち込まない（要請②の放棄）。要請②に置き換えるべき仮定として本稿が主張する要請は以下の②′である。

②′真空中では、光は光源の座標系を基準に一定の速さｃで伝播する。

つまり、『光はその光源からの速度を光速度に保つ』という要請である。この主張は１９世紀にも“一定射出速度の仮説”としてリッツによって提唱された。しかし、その当時はあくまでもエーテルを前提とした仮説であり、媒質を伝わる波としては受け入れられないという拒否反応や、二重星の観測結果が否定的であるという理由からあまり議論されずに衰退していった。本稿は再度このリッツの一定射出速度の描像を、光は量子であるとする現代物理の観点において議論することを提唱する。つまり、①および②′の二つの要請から出発することを主張するものである。この要請は光源に対し相対速度を持つ観測者から見ると、光が光速度ｃを越えて観測されることもあり得ることを示している。これは“光速度を越える現象はあり得ない”とする現代の常識に真っ向から対峙する。しかしながら、この非常識は１００年前は常識であった。むしろ、特殊相対性理論の要請こそが非常識であったのだ。そして１００年前、常識に捕らわれないことの重要性を説いたのはアインシュタインその人であった。

２．光が伝播する様子

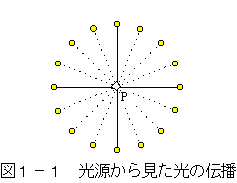
　　要請②と要請②′において、光の伝播する様子がどのように異なるかを明確にしておく。まず光源Ｐと共に等速度で移動する慣性系では、要請②も要請②′も共に図１－１のごとく、射出された光は光速度で等方に伝播するのを観測する。

　これに対し、速度ｖで移動する光源を地上から観測した光の伝播の様子を図１－２に示す。(a)は、光速度不変の原理にもとづく光の伝播の様子である。Ａ点で放射された光は光源の移動速度とは無関係にＡ点を中心に光速度で伝播する。ただし、その伝播は完全に等方的ではなく、前方が密、後方が粗となる。これは移動方向に対して垂直の向きに放射された光は、光源がＢ点に到達したときもその鉛直線上に存在するという解釈のためである。この解釈は、アインシュタインが時間遅れの現象を説明するのに好んで使用した、天井と床を往復する光時計を搭載した列車の仮想実験でも採用されている。また1728年、イギリスの天文学者ブラッドレーが観測した光行差の現象においても立証されている。

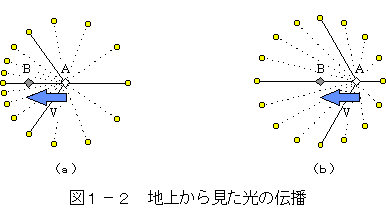
　一方、(b)は一定射出速度の仮説にもとづく光の伝播の様子である。Ａ点で放出された光は、光源の移動とともに速度ｖの移動速度を継承し、常に光源に追随して移動する。光は光源を中心に等方的に広がり、光源からは図１－１のように観測されることが明らかである。すなわち一定射出速度の仮説は、等速度で移動する爆薬がその途中で炸裂した際の破片のごとく光が放射されることを主張している。その運動学的様子は、ニュートン力学の範囲内で解決する。それに対し、(a)の伝播は、光源において図１－１のような観測を得るため、地上からの観測で認められる進行方向前後における光の粗密性を打ち消し、更に光源においても光が光速度で伝播することを整合すべく、時空に対するローレンツ変換を必要とする。

　この２つの伝播の差異は、静止系である地上から見て、等速度ｖで移動する光源から一定周期で光が発信される場合により明確になる。図２は、要請②と要請②′のそれぞれにおいて、一定間隔の光の発信がどのように伝播するかを示している。

　まず、図２(a)は、光速度不変の原理である要請②に基づいた伝播の様子である。それぞれのタイミングで発信される光は、地上から見ても光速度で四方に発信されるはずであるから、同心円にはならない。この波紋の形状は、地上から観測すると音波のそれと同様である。しかし、光源と等速度で移動する観測者にとっては、同心円として観測されるはずである。この両者を整合するためには、速度ｖで移動する座標系と静止座標系との間に同時性のずれを導入する必要がある。そして、特殊相対性理論においては、この同時性のずれから始まり、固有時の設定、ローレンツ短縮と次々と複雑な機構を持ち込まなければならない。

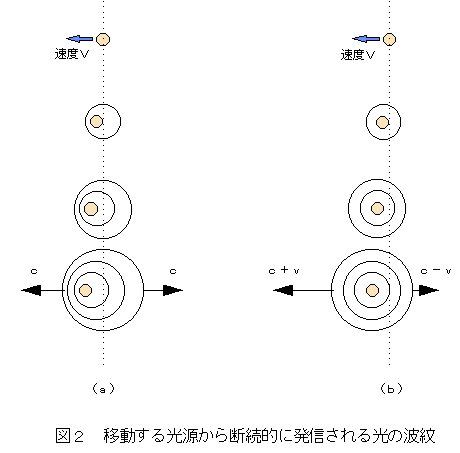
　しかし、要請②′においてはそのような機構を導入する必要はない。光の断続的な発信は、図２(b)のように地上にいる観測者にとって同心円状に広がり、光源と等速度で移動する観測者にとっても全く同じように観測される。ここに同時性のずれなどという概念は不要である。当然ローレンツ短縮も観測されない。ただし要請②′を前提にすると、地上の観測者にとっては、進行する光源の前方では光速度ｃ以上の速度(c+v)で光が伝わり、逆に後方においては光速度ｃ以下の速度(c-v)で光が伝わることになる。極端な例として、光速度を越えて移動する光源の後方には、光が伝播しないことになる。
　だが、この現象は果たして信じ難いことであろうか。アインシュタインはこの現象をあり得ないことと考えた。しかし光が光子という運動量をもつ量子であることを思い起こすとき、決して非現実的な現象ではない。電磁気学的に考察すると、仮に光源が光速度に達したとき、その後方には次第に弱まっていく脈動しない電界あるいは磁界が存在する場としてとらえることで、何の矛盾もないと考える。

３．量子としての光

　　アインシュタインは、光をｈνのエネルギーをもつ粒子ととらえる事を主張し、光電効果の説明に成功した。この事は、光が波動と粒子の両方の性質を合わせ持つ量子であることを示している。一方、1924年にド・ブローイが提唱したように、従来粒子としてとらえられてきた電子も、干渉や回折といった波の現象を確認することができる。結局、電子に代表される素粒子も、電磁波である光も、共に量子という枠組の中でとらえられることは、現代物理学においては周知の事実である。
　本稿の主張は、電子波において誰もがその媒質を問わないように、光においても問う必要はないのではないかという事である。エーテル仮説は光の波動性に関して、あくまでも古典的な波の描像(音や地震、水面における波など)でとらえようとした発想であった。電子波はいわば確率波であり、同様に、電磁波も光子における一種の確率波ととらえるべきであると主張する。この考え方は量子電磁気学(QED)で採用されており“くりこみ”という人工的な処理を施すとはいえ、磁気モーメントの算出において下記のような高精度な値をはじき出している。

　　　理論値：1.00115965246
　　　実験値：1.00115965221

この量子電磁気学における理論骨子の中では、特殊相対性理論は一切使用されていない。また、光を対象とした理論であるにもかかわらず、ローレンツ変換は全く採用されていない。にもかかわらず上記のような精度ある予測が立てられるのである。少なくとも、光を光子としてとらえ物理現象を説明する場合は、特殊相対性理論が主張する諸々の効果を必要としていないことがわかる。それどころか、ＱＥＤは光子が光速度ｃを越えて伝播する現象をも想定している。

→『光と物質のふしぎな理論』(p.123)R.P.ファインマン著<岩波書店>

　さて、電子の粒子的側面においてその運動力学的ふるまいがガリレイの相対性原理に従うことは誰も疑わない。同様に、電子の波動的側面においても“電子波速度不変の原理”(電子線はそれを発生する機器の運動によらず観測者において一定の速度をもつ)を主張する人はいないであろう。電子は明らかにその発生源からの速度を相対的に維持するのである。　もし、光を電子と同じように量子的に扱うのであるならば、光の速度はその光源からの速度を相対的に維持すると考えるべきである。このように、光子も電子と同様な量子のひとつととらえることで、要請『②′真空中では、光は光源の座標系を基準に一定の速さｃで伝播する。』は、妥当なものと判断できる。

４．マイケルソン・モーレーの実験

　　マイケルソン・モーレーの実験で干渉縞が現れなかった事実は、光の速度が光源を基準に光速度で伝わるという要請②′からみれば、あまりに自明となる。マイケルソン・モーレーの実験は、光源と観測点の相対速度は完全に一致しており、要請①および要請②′から、干渉稿は出現するはずはない。
　仮に、マイケルソン・モーレーの実験を光ではなく電子線で行った場合、そこに干渉縞が現れない事は明らかである。本稿は、光子を他の量子に対して特別扱いすることなく、至極単純な要請②′を仮定することで、ローレンツ収縮のような複雑な機構を導入せずに、マイケルソン・モーレーの実験事実を説明することを主張する。

５．磁界の相対性

　　今、図３(a)のように電荷ρを帯電している導体が、地上の静止座標系に対して速度ｖで運動しているとする。この時、地上に固定された観測点Ｓ１では、紙面に垂直の方向に磁界が現れることが観測される。一方、図３(b)のように、地上に対して電荷ρが静止しており、観測点Ｓ２が地上に対して速度－ｖで移動している場合も、観測点Ｓ２には紙面に対して垂直の磁界が現れることが観測される。

→『電磁気学ノート』(p.176)藤田広一著<コロナ社>

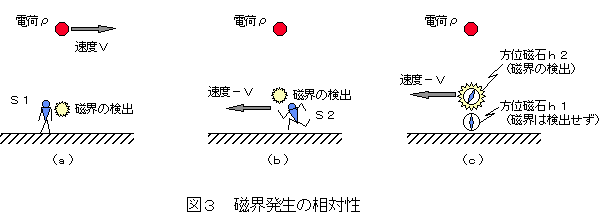
　このように磁界は空間に与えられた絶対的な属性ではなく、それを発生する発生源とそれを観測する観測点の相対速度によって検出できる物理量である。この分析は、モノポールが存在しない理由を提示しているとも考えられる。
　磁界が電荷(電界)と観測点の相対速度に依存することを明確に示す思考実験を図３(c)にて行ってみる。電荷ρと方位磁石ｈ１は、ともに地上の静止系に対して静止しているものとする。このとき、ｈ１の磁針は動かない。さて今、方位磁石ｈ１の近傍を方位磁石ｈ２が速度－ｖですり抜けた時、それぞれの方位磁石には何が起こるであろうか。方位磁石ｈ１は何事もなかったかの如くその磁針が振れないのに対し、方位磁石ｈ２は電荷ρとの相対速度により磁針が振れるであろう。すなわち、同一の空間において、磁界は存在と不在の両方の現象を示すことがわかる。光は電界と磁界の脈動が交互に繰り返される電磁波である。したがって、光もそれを観測する運動の状況によって、その状態が変化することは容易に想像できる。特殊相対性理論の要請②は、それを否定し観測点がどのような運動状況にあっても、光の状態は一定であることを主張している仮定である。これは本節の思考実験と明らかに矛盾する。

６．波動方程式の基準座標系

　　特殊相対性理論における要請②設定の論理的根拠の一つに、マックスウェル方程式から導出された電磁波の波動方程式が、あらゆる慣性系で成立するはずであるという主張がある。すなわち、

　　　E = A･sin((2π/λ)･(x－ct))

なる電磁波の波動方程式は真空中の静止した座標系に関して記述されており、その波動の速度は、式中のｃで表されるという考察である。さらに速度ｃは、

　　　c = (εo･μo )^(-1/2)

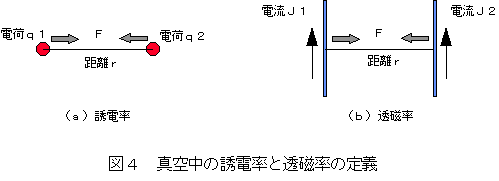
にて与えられ、これが普遍定数で組み上げられているにもかかわらず、あらゆる慣性系で成り立つことが、要請②を導く根拠となっている。この論旨展開を検証するために今一度、εoの定義、μoの定義から再考してみたい。まず、εoの定義であるが、これは図４(a)のごとくq1およびq2の２つの電荷がrだけ離れた位置に配置されたとき、互いに働く力Fの関係式で定義される。

　　　F = (1/(4πεo))･(q1･q2/r^2)

すなわち、ともに１クーロンの電気量を持った物体を１メートル離しておき、その間に働く力をニュートン単位で計れば、(4πεo)が求められる。ここには、運動学的な背景が存在しない。しかし問題は１クーロンの定義である。１クーロンの定義は、１アンペアの電流を１秒間流したときに運ばれる電気量と定義されている。ではここでいう１アンペアの定義はどのようなものであろうか。１アンペアを定義するには以下のような磁気の法則を利用している。

　　　F = (μo /(2π))･(J1･J2/r)

すなわち図４(b)のように、等しい強さの直線電流が１メートル離れて平行して流れるとき、その１メートルあたり２×10^(-7)ニュートンの力が働くときの電流を１アンペアと定義している。この定義から逆に、 μoは４π×10^(-7)と規定されている。

　このように、１アンペアは電流間の力から定義され、それから決まる１クーロンを使って電気的な力を計るとεoが決まり、それを組み合わせたものが電磁波の伝播速度ｃを与えるということになっている。こうしてみると、伝播速度ｃの導出は、電流間の力の定義から出発していることがわかる。そこで、この電流間の力、すなわちローレンツ力を今一度検討してみたい。
　今、図５(a)のように、互いに平行して電荷e1と電荷e2が等速度ｖで並進している状況を想定してみよう。一見、この状況でローレンツ力が働くように思考しがちであるが、ここにはローレンツ力は働かない。図５(a)は、互いに等速度で移動している電荷同士であるから相対速度はゼロであり、前節の電界と磁界の相対性で論述したとおり、アンペールの法則にもとづく磁界の検出はみられず、したがってローレンツ力も検出されない。仮にこの状況でローレンツ力が働くのであれば、太陽に対し時速10万Kmで高速な公転運動をしている地球上のあらゆる電荷の間には、ローレンツ力が検出されるはずである。

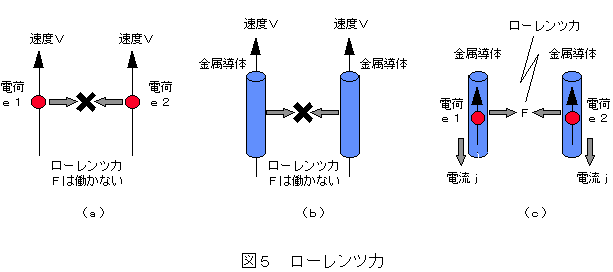
　同じ理由で、図５(b)のように互いに平行な金属導体が等速ｖで並進している場合にも、ローレンツ力は働かない。もし働いたら、地球の公転方向に向きをそろえた金属導体はあたかも磁石のようにベタベタとくっつき合うはずである。しかるに図５(c)のように、金属導体に同じ向きの電流ｊを流した場合、そこには明らかにローレンツ力Ｆが働く。ここには電流というものの基準座標系を厳密に定義しなければいけないという示唆が与えられている。電流は、それが流れる金属導体、すなわち金属の原子核の静止座標系を基準に測定されるものであるということである。
　波動方程式における伝播速度ｃは、電流間の力から導出されているのであり、電流とはそれが流れる金属導体の座標系を基準にしているのであるから、マックスウェルの方程式は、すべての慣性系で同一の伝播速度ｃを与えているわけでないことがわかる。そこで与えられる伝播速度ｃは、あくまで１アンペアという電流量を定義できる慣性系、すなわちローレンツ力を検出できる座標系を基準にした速度である。そして一般に、光源の座標系は上述の金属導体の座標系と一致する。すなわち、『②′真空中では、光は光源の座標系を基準に一定の速さｃで伝播する。』という事実を示している。

７．電磁波の伝播

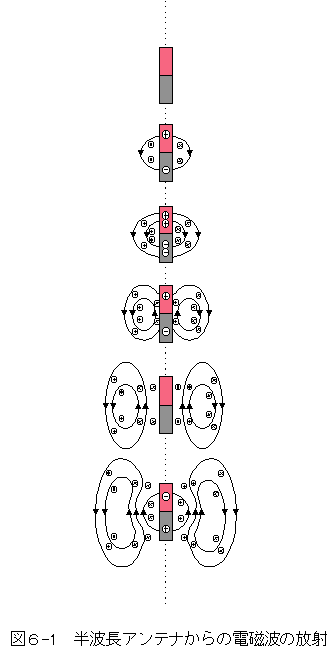
　　光、すなわち電磁波が発生する状況を図解してみる。図６－１は、半波長アンテナから電磁波が放射される模様である。図中の曲線矢印は電界を表し、紙面に垂直に発生する磁界は◎と×で表現している。

→『電磁波とはなにか』(p.142)後藤尚久著(講談社)

　今、半波長アンテナが静止座標系である地上に対して、速度ｖをもって移動しながら電磁波を放射する場合、地上からこの電磁波を観測するとどのように見えるかを考察してみる。まず、特殊相対性理論の要請②にもとづいた図解が図６－２である。電磁波の伝播は、半波長アンテナの速度に無関係に、地上から見て光速度ｃで広がるはずである。

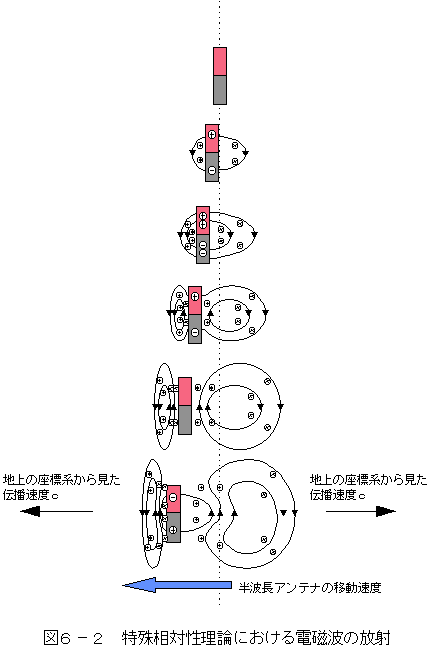
　この電磁波の伝播は、図１－２(a)で検討した進行方向に対しての光の粗密状態を裏付けている。移動する光源から放射される電磁波を地上から観測すると明らかに前方の電磁波は密になり、後方の電磁波は粗になる。
　この電磁波の伝播の様子は、まるで、地上の座標系に張り付いたエーテルという媒質の中を電磁波が広がっているように見える。特殊相対性理論の主張は、エーテルの存在を否定しているように見えるが、実は各座標系に固有に存在するエーテルを想定しているとも解釈できる。そのエーテルは各座標で独立に存在しているため、光速度は各座標で常に一定の速度ｃで観測されるのである。しかし、このように各座標ごとに存在するエーテルという概念を物理的に矛盾無く説明するためには、たとえ実存としてのエーテルを否定しそれを時空と呼び換えたとしても、各座標系に対する固有時を設定したり、各座標系間の同時刻に相対性を導入したりしなければつじつまが合わなくなる。特殊相対性理論は、光速度一定の原理のもと、これらの現象を論理的に導出した理論である。その導出過程は数学的にも物理学的にも完全である。ただし、各座標系に固有のエーテル(時空)が存在し、しかも各々のエーテル(時空) 同士は全く干渉しないという仮定が正しければである。
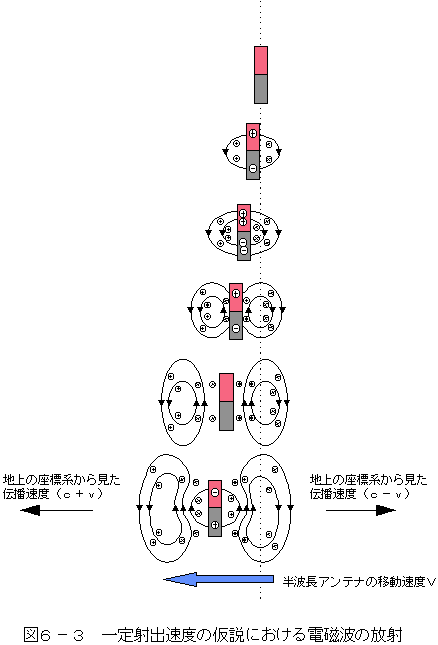
　一方、本稿の要請②′、すなわち一定射出速度の仮説にもとづいた図解が図６－３である。電磁波は半波長アンテナの速度ｖを継承して広がる。電磁波は移動している半波長アンテナを中心に、一定の速度ｃで広がる。これを地上から観測すると、前方の光の速度はｃを越えた速度(c+v)で伝播し、後方の光の速度はｃに満たない速度(c-v)で伝播することを示している。

“これは、明らかに要請②とは相いれない。しかしこの要請②′は、静止物体に対するマックスウェルの理論にもとづいて、運動物体の電気力学を簡単にかつ一貫して建設するためには十分である。いま考えている立場によると、特別の資格をもつ絶対静止の空間の存在は必要ではなく、また電磁過程の起こる空間に絶対速度ｃを仮定しなくてもよい。このような意味で、「光のエーテル」も「光速度一定の原理」も導入する必要はない。”

→（アインシュタインの論文の冒頭部を一部流用）

８．検証

　　本稿の主張を直接実験により検証するのは、多くの困難が存在する。光速度ｃは科学技術の発達した今日においても、やはりかなり高速だからである。我々が人工的に実現できる最高速の光源であっても、光の速度と比べると、実験誤差に打ち勝つにはかなりの工夫を必要とするであろう。事実、特殊相対性理論を擁護する多くの観測結果例は、光速度一定の原理を直接示したものではなく、そのほとんどが導出された現象(質量の増加や時間の遅れ) に対して与えられている。
　しかし、本稿の主張を検証するのは、地動説と天動説の真偽を判定するほど不可能な話ではない。地動説と天動説はマッハの原理から言えば共に正しく、ひとえに地動説の方が天体の運行を簡素に表現できるという審美眼的判断基準で選択されているにすぎない。むろん科学において、より簡素な法則への統一志向は正しい姿ではある。自然は単純を好む。しかしその真理を把握しきれないとき、人間はしばしば複雑な表現をしてしまう。
　しかるに、要請②と要請②′は、どちらかが正しく、どちかかが誤っているのである。ここで、メスバウアー効果を利用した振動数の変化(ドプラー効果)を検出する実験を考えてみる。ドプラー効果を例に取る場合、音波の場合から考え始めると基準座標系の意味が明確になる。なぜならば、音波は空気という媒質の振動であるため、音源と観測点との相対速度だけでは効果が確定せず、空気との相対速度も考慮する必要があるからである。
　今、観測点と音源が相対速度ｖで近づく時、それぞれの空気に対する速度の絶対値をｖ１、ｖ２とすると、

　　ｖ＝ｖ1 ＋ｖ2　　・・・・(1)

が成り立つ。
この時、振動数νoの音波は以下のような振動数の変化を生じる。

　　ν ＝ νo･( (c＋v1)／(c－v2) )　　・・・・(2)

　これに対し、特殊相対性理論の主張および本稿の主張は共に要請①を仮定しているため、静止している光源に向かって観測点が近づく場合でも、逆に静止している観測点に向かって光源が近づく場合でも同じ効果を生じる。したがって、式(1)のように各々の媒質(空気やエーテル)に対する速度に分解する必要はなく、相対速度ｖのみを考慮すればよい。しかし要請②と要請②′は、波動の基準座標系の解釈が大きく異なる。これは、前述の図２を参照すれば明らかである。それぞれの波動がどのような座標系を基準とするかは以下のとおりである。

　　・音波の場合（古典的な波の場合）：空気
　　・特殊相対性理論（要請②の場合）：観測点
　　・本稿の主張（要請②′の場合）：光源

　ここで、音波のアナロジーで要請②と要請②′の基準座標の差異を明確にしておく。まず要請②の場合は、空気が観測点に張り付いたように移動し、音源はその風を受けて音波を発生する場合にたとえられる。観測点側は常時無風の状態であり、音の速度は常に一定に観測される。しかし実は音源の座標系でも無風である、というのが特殊相対性理論の主張である。
　これに対し要請②′の場合は、空気が音源と共に等速度で移動する場合である。したがって、観測点側では風を受けながらそれに乗っている音を観測することになり、音の速度は音源の速度(＝風の速度)が加算された形で検出される。一方、音源は常時無風状態であり、音源側からすれば音速は常に一定となる。ただし以上はあくまでも、それぞれの波動の基準系を説明するためのアナロジーであり、実際には、要請②も要請②′も波動の媒質(エーテル)を前提としていない。従来の光速度に関する議論は、エーテル仮説を肯定する主張(音波の場合)と、それを否定する主張(特殊相対性理論)の対比で語られ続けてきた。本稿は、波動の基準座標系に着目し第三の説を提示するものである。
　さてここで、実際に特殊相対性理論のドプラー効果を導出してみる。この時の光の波動は、常に観測点の座標を基準にしているため、式(2)における分母の項だけが作用することになるが、光源が速度ｖで移動しているため、時間の遅れ（１－(ｖ／ｃ)^2）^(1/2)が生じてその分が振動数の変化に乗じられる。

　　ν ＝ νo･c／(c－v) × ( 1－(v／c)^2 )^(1/2)
　　　＝ νo･( (c＋v)／(c－v) )^(1/2)　　・・・・(3)

　一方、本稿の一定射出速度の仮説では常に光源の座標を基準にしているため、式(2)における分子の項だけが作用することになる。そして時間の遅れは存在しない。

　　ν ＝ νo･(c＋v)／c　　・・・・(4)

ここでνoを１としたときの、式(3)および式(4)による振動数の変化を図７に示し、特殊相対性理論と本稿の主張を定量的に議論する。

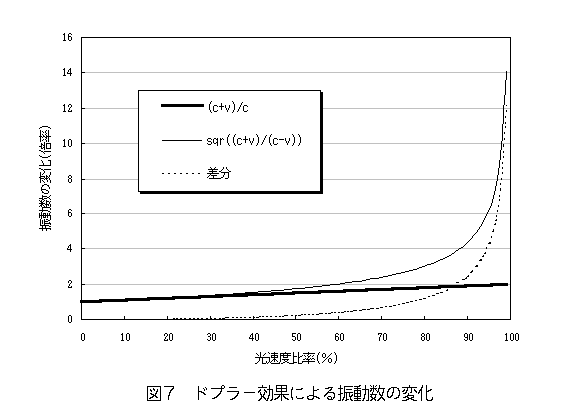
　図７が示すとおり、一定射出速度の仮説によるドプラー効果は線形性をもっており、特殊相対性理論のそれとは明らかに異なる。しかし破線で表された差分を見ればわかるように、定量的には光源の速度が充分高速でなければ要請②と要請②′の差異を認めにくい。式(1)および式(2)の計算によれば、 νoを100％として両者の振動数変化を高々0.00005％検出するためにも、光源を光速度の 0.1％もの速度（時速1億Km）で移動する必要がある。光速の30％以下の速度において要請②と要請②′との振動数の変化の差を検出するには、ドプラー効果(振動数の変化) そのものの検出に比べ、対数的におよそ２倍の精度が要求される。
　このように、ドプラー効果の観測例一つをとっても、その振動数の変化が、要請②を裏付ける数値なのか、要請②′を裏付ける数値なのかを、誤差範囲内で特定するのは難しい。この困難を解消するためアインシュタインは、横方向からの観測で通常のドプラー効果をゼロに押さえ込むことを提唱した。このアイデアを利用した実験をアイヴスが行ったが、結局直接観測したのは縦方向のドプラー効果であり、算術平均という演算処理で縦方向のドプラー効果を相殺したにすぎなかった。
　しかしここに、振動数の変化を10^(-10)の精度で検出できる実験装置があるならば、直接的な検証の方法がある。それは、人工衛星を利用する方法である。現在打ち上げられている静止衛星は、高度36000Kmの上空をほぼ１日で周回している訳であるから、地球座標系に対し時速1万Kmで移動していることになる。もし、これとは逆方向に周回するもう一つの周回衛星を打ち上げ、ほぼ同一の軌道を与えれば、１２時間毎に時速2万Kmですれ違うことになる。この相対速度で光を放ちそのドプラー効果を検出すれば、振動数の変化は要請②と要請②′ において10^(-10)程度の差を生じるはずである。この差を検出することで、一定射出速度の仮定が正しいことを検証できる。

９．周回衛星のパラドックス

　前節で議論した検証方法は、特殊相対性理論に対する新しいパラドックスも提示している。互いに高速ですれ違う周回衛星は、各々地球に対して無限に落下している慣性系である。本稿が提案するパラドックスは、これら２つの慣性系の時間進度に関するものである。２つの衛星は１２時間毎にすれ違うことになるが、はたして各々の時計はどちらが進んでいるのだろうか。お互いにとって相手は高速で移動している。しかも、この２つの系は自由落下という完全な慣性系の中にあるのである。
　このパラドックスは、双子のパラドックスのように加速プロセスを前提としないので、特殊相対性理論を検証する上で、より適した思考実験になりうる。

補足

【Ａ】アインシュタインの主張

　以下は、有名なアインシュタインの特殊相対性理論の論文の冒頭であり、その二つの要請を設定しているくだりである。この原文を読む限り、要請②はあまりに唐突に設定されているように見える。この要請②を要請②′に置き換えても、矛盾のない論理の展開が行えると筆者には思える。

『マックスウェルの電気力学は、運動物体にあてはめた場合、現象の種類には無関係に、対照的でない結論を導く。たとえば、磁石と蓄電器のあいだにおこる交互の電気力学的作用をとるとしよう。この場合観測される現象は蓄電器と磁石の相互の運動だけに依存して決まる。ところが、従来の考えによると、これら二つの物体のどちらかが他に対して運動している場合と、その逆の場合とで、明確な差があるとされていた。もし磁石が運動し、蓄電器が静止しているときには、磁石のまわりに一定のエネルギーをもつ電場が生じ、そのために蓄電器のある場所に電流が流れる。その反対に磁石が静止し、蓄電器が運動しているときには、磁石のまわりに電場は生じない。しかし、蓄電器のなかには最初の場合の電気力によって生じたと同じ方向の強さの電流が生じる。もちろん、この二つの場合の相対運動は等しいとする。
　このような例と、さらに“光の媒質”に対する地球の相対運動を発見しようという試みの失敗とを合わせて考えると、電気力学の現象は力学の現象と同様に、絶対の静止という考えを立証するような性質を持っていないように見える。むしろこれらの事実から、力学の方程式が成り立つすべての座標系に対して、電気力学や光学の法則がいつも同じ形で成り立つと考えられる。このことは、小さな物理量の１次の近似についてはすでに立証ずみのことである。
　このような推測を第一の要請とみなして、相対性原理とよぶことにする。さらに次のような第二の要請をつけ加えよう。

　光は常に真空中を一定の速さｃで伝播し、この速さは光源の運動状態には無関係である。

　これは、ちょっと考えると、第一の要請とは矛盾するように見えるかもしれない。しかしこれら二つの要請は、静止物体に対するマックスウェルの理論にもとづいて、運動物体の電気力学を簡単にかつ一貫して建設するためには十分である。いま考えている立場によると、特別の資格をもつ絶対静止の空間の存在は必要ではなく、また電磁過程の起こる真空の１点に一つの速度ベクトルを仮定しなくてもよい。このような意味で、“光のエーテル”を導入する必要はないことがわかるであろう。
　これらか述べる理論は、すべての電気力学と同様に剛体の運動学にもとづいている。なぜならば、この種の理論の主張は、剛体(座標系)、時計、およびいろいろの電磁過程のあいだの関係について触れるものだからである。これらの関係についての考慮が従来不十分であったということが、現在の運動対の電気力学に内在する困難の原因なのである。』

→“運動している物体の電気力学について”(アインシュタイン)
Zur Elektrodynamik bewegter Korper Ann. der Phys 17(1905),pp.891～921

【Ｂ】特殊相対性理論を裏付ける観測例

　さて本節では、特殊相対性理論が正しいとされる裏付けの例を、筆者の知りうる限り掲げておく。これらは定量的な検証として述べられているが、既に議論したように、驚異的に高速な光の速度を相手に、その実験誤差を解消できているのか疑問ではある。しかし、これら一つ一つに対しその不具合点を洗い出し、別の解釈をあてはめていくということは行わない。筆者自身、特殊相対性理論における時空の統一的解釈や、日常の常識を覆すその現象の導出に胸打たれた一人であり、自然界の真理がやはり光速度一定の原理を示すのであれば喜んで納得する。
　だが、もし一定射出速度の仮説が正しければ、特殊相対性論にまつわる多くのパラドックス(双子のパラドックスや周回衛星のパラドックスなど)は一掃され、量子力学と特殊相対性理論との矛盾も解消することを付け加えておきたい。

(1)二重星からの光の観測
　二重星というのは、二つの星がともにそれらの重心のまわりを回っているものである。一定射出の仮説によれば、地球に向かって近づきつつある方の星が射出した光は、遠ざかってゆく星から射出された光に比べて進行が速くなる。しがたって、二重星の軌道には、みかけの不規則性が現れるはずである。ド・ジッターが1913年に行った二重星についての観測では、このような不規則性は見られなかった。

→『双子のパラドックス』(p.50)Ｌ．マーダー著<講談社>

(2)メスバウアー効果
　ルドルフ・メスバウアーは1958年、原子核は事実上反跳を受けずに、電磁波をγ線の形で放出することがあることを発見した。これは、信じられぬほどの高精度で、一定の振動数の放射線を得られることを示している。この事を利用し、γ線の発生源である原子核を回転台に設置し、ある距離を置いて同種原子核によりγ線が共鳴吸収される量を観測した。すなわち、回転台で与えられるγ線の発生源の速度により、どのように振動数が変化するかを共鳴による吸収量で把握しようとした。回転の速度をいろいろ変えて観測した結果、その変化量は特殊相対性理論による計算と一致した。

→『双子のパラドックス』(p.238)Ｌ．マーダー著<講談社>

(3)横ドプラー効果の観測
　移動する物体から発する波を進行方向と正確に垂直の方向から観測した場合、ニュートン力学においてはドプラー効果が検出できないはずであるが、もし特殊相対性理論が正しいとすると、移動速度に応じた時間の遅れにより振動数の変化が観測されるはずである。ベル電信研究所のＨ・Ｅ・アイヴスは、1938年、高速で走っている水素原子の流れであるカナル線から放出されたスペクトル線の振動数の変化を測定した。この際使用したカナル線管は、デンプスターが1932年に粒子の速度をほぼ一定に保つように改良したものである。また、カナル線の方向に正確に直角の方向から測定する必要があったが、これはカナル線を直角の方向から測定せず、カナル線の運動方向およびその反対の方向の２つの方向から放出されるスペクトルを測定し、その算術平均をとることで解決した。古典論で現れるドプラー効果は、算術平均を取ることで相殺されることがわかったからである。そこで相殺しきれない振動数の変化が純粋な横ドプラー効果のはずである。古典論では起こり得ない横ドプラー効果が観測され、その値は特殊相対性論が導出した時間の遅れにほぼ一致することが確かめられた。

→『物理空間とは何か』(p.118)井田幸次郎著<三省堂>

(4)μ中間子の寿命の延び
　宇宙から高速で飛来するμ中間子の寿命が、1940年代に多くの機会で測定された。その方法は、中間子の数を高い所と低い所でかぞえて比べることである。Ｂ・ロッシ、Ｎ・ヒルベリー、Ｊ・Ｂ・ヘーグは、高度差のあるコロラドの３カ所にて測定を行った。測定場所は、エバンス山(4300ｍ)、エコー湖(3240ｍ)、デンバー(1616ｍ)である。カウントは、検出器の前に炭素の吸収体を置いた場合と置かない場合の両方について行った。この吸収体は、高度の違いによる空気層の吸収能力を調整するため設計された。違った高度における“吸収体を置いた場合” のカウントの差が、その途中で起こったμ中間子の崩壊数をあらわすことになる。結果は4300ｍの高度で存在した中間子の６０％が1616ｍまで崩壊せずに生き残った。この結果は、μ中間子は静止している時よりも高速で走っている時の方が、明らかに長い寿命をもつことを示す。 μ中間子の静止寿命は約2.2×10^(-6)(秒)が採用されている。静止寿命から算出すると、たとえ光速度ｃで中間子が飛来しているとしても、 660ｍしか進めないはずが2700ｍの距離を進んだことになる。これは特殊相対性理論により高速で飛来する中間子の時間の進度が遅くなったことを示す。

→『双子のパラドックス』(p.100)Ｌ．マーダー著<講談社>

(5)π中間子のγ線崩壊
　ジュネーブにてアルヴェーガーら４人の研究者がセルン (西欧合同原子核研究所)の陽子シンクロトロンでつくられた中性π中間子の自然崩壊の結果生まれるγ線を観測した。π中間子は極めて短命であり、 10^－16(秒)程度の寿命しか持たず、すぐに２個のγ線粒子に自然崩壊する。かれらは、π中間子の速度が光速の約99.75％に達することを確認した。それでも非常な速度で走るこれら中間子から生まれるγ線の速度が、 0.01％の誤差で光速度ｃに等しいことがわかった。すなわち２次的に発生したγ線の速度は、その源である中間子の超高速度とほとんどわずかしか違っていないということである。これは、速度の加法測においても、光速度を越えることが出来ないという特殊相対論の主張を裏付けている。

→『双子のパラドックス』(p.59)Ｌ．マーダー著<講談社>

(6)電場による電子の加速実験
　真空の容器内に正と負の電極をある距離をおいて配置し電場を発生させる。その間に多量の電子を発生させると、その電子群は負極から正極に向かう。電場の強さを徐々に上げていくと、ニュートン力学では電子群の得る速度は線形に上昇するはずであるが、いかに電場の強さをあげても電子の速度は光速度ｃを越えることなく、ｃに漸近した。これは物体の速さに限らず、すべての信号や作用の伝達速度が光速以上になり得ないという特殊相対論の主張を裏付けている。

(7)カウフマンの実験
　二枚の金属板を平行に置いて、一方に正、他方に負の電気を帯びさせる (平板コンデンサー)。そしてその間に電子を入れれば電子は負電荷を帯びているから、正に帯電した板(陽極)の方に引かれる。このことは電子が走っていても変わらない。電子線の行先に蛍光塗料を塗ったスクリーンを置けば、電子が当たった点が光るのでその点の位置から電子がどのくらい曲げられたかを知ることができる。一方、板の大きさ、与えた電気量および電子の速さから、電子の軌跡の曲がる割合が計算できる。そこで電子の速さを徐々に増してこの実験を繰り返すと、速度が小さいうちは実験値と計算値が一致するが、速度が次第に増して光速度に近づくと、実験結果の方が曲がり方が少なくなった。この事実より、電子の質量は速度と共に増加していると結論される。

→『相対性理論はむずかしくない』(p.60)中野董夫ら著<講談社>

(8)素粒子の反応における質量とエネルギーの換算
　π中間子は、π(140) → μ(106)＋ν(0) のようにμ中間子とニュートリノに崩壊する。ここで括弧内の数字に、メガ電子ボルト単位でそれぞれの静止質量を与えた。反応後の静止質量の総和が反応前に比べ減少しているが、これはμ中間子とニュートリノの運動エネルギーに還元されたと考えられる。また、π中間子と陽子を衝突させると、Σ粒子とΚ中間子に変化する反応が起こる。 π(140)＋ｐ(938) → Σ(494)＋Κ(1189) この場合は、反応後の静止質量の総和が反応前に比べて増加しているが、これはπ中間子と陽子の運動エネルギーがΣ粒子とΚ中間子の質量に転換されたと考えられる。このように、特殊相対性理論が導出したＥ＝ｍｃ^2の式で表される質量保存側とエネルギー保存側の統合的解釈により、素粒子反応の現象をとらえることができる。

→『相対性理論はむずかしくない』(p.152)中野董夫ら著<講談社>

(9)原子時計の時間の遅れ
　世界各地の原子時計を同期させるため、ジェット旅客機に原子時計をのせて運ぶ実験が行われた。この原子時計はおよそ時速1000kmで約１０時間飛行するうちに、１億分の２秒ほどの遅れを生じた。この事実は、高速で移動する座標系の時間の遅れるという特殊相対性理論の効果を実証するものと考えられる。

　以上の９つの事例における現象は、現在特殊相対性理論の効果の表出として説明されているが、もし一定射出速度の仮説が認められれば、それに準じた解釈を与え直す必要がある。その再解釈プロセスの中で、従来は特殊相対性理論の効果として片づけられていたために見落とされていた新たなる発見が、これらの物理現象の中に秘められている可能性がある。

【Ｃ】時間についての考察

　筆者は“時間”というパラメータが物理的実存として組み込まれている理論には懐疑的である。“時間”は物理的な予測表現をするための数学的手法にすぎないと考えているからである。すなわち、「時間は実存しない」というのが筆者の持論である。

　時間はしばしば、“時間”という数直線が存在しその上を実体が移動しているかのようなイメージで語られる。あるいは、あたかも過去や未来が現在の両側に連続して存在している映画フィルムのようなイメージが与えられる場合もある。しかし我々は決してフィルムの他のコマに移動できないし、時間数直線を負の向きに移動することもできない。時間は未来に向かって一方向性を持っているという解釈は、その背景に時間の基準軸を想定しており、半ば絶対時間の存在を肯定しているように思える。方向性以前に、時間そのものが存在しないのであり、タイムマシンや因果律のパラドックスに関する議論は、このように本来存在しないものに対して行われ続けているのである。

　過去は我々の記憶の中にのみ存在し、未来は我々の予測の中にだけ存在する。人の記憶と予測の能力が優れているために、時間が実存しているかのような錯覚に陥っているのだ。時計の秒針は時を刻んでいるように見えるが、等速で移動しているにすぎない。１秒後には１秒前の位置に秒針が存在しないというだけの話である。しかし、ここで思わず“１秒”という表現を利用してしまったように、時間という単位は物理的な事象表現になくてはならないパラメータである。これが時間の実存性を自明のことと錯覚する要因にもなっている。だが、数学上で設定する全てのパラメータが物理的に実存するわけではないように“時間”もまた実存しないと考える。

　エントロピー増大の法則に従った“熱力学的時間の矢”という概念があるが、物理学の根本的な原理は単一の素粒子にも適用可能であるべきであり、時間実存の議論の中に統計力学的要素を持ち込むべきではない。ここに、いくつかの仮想実験を提示したい。

[1]　もし、宇宙空間に存在する全素粒子が動きを止めたら、はたしてそれでも時間は進行しているのであろうか？　それとも停止しているのであろうか？

[2]　この宇宙の全素粒子が偶然にも１年前と同じ座標配置と運動量になったら、それでも今年は今年なのか？　それとも、それは１年前なのか？

[3]　観測者も含めて全宇宙の時間進度が半分に遅くなったら、果たしてそれを知覚できる者がいるであろうか？

仮想実験[1]は空間の実存も脅かす実験である。なぜなら[1]の命題を発展させると「素粒子が１つも無い宇宙空間は、空間を定義できるか」という命題を導くことになるからである。この状況下においては空間スケールの定義さえ不可能となる。しかしこのような宇宙は、そもそも物理学の対象ではない。物理法則の記述の必要性そのものがないからである。
　物理学の対象は、「素粒子が１つだけある宇宙空間」から始まる。その素粒子には質量と占有空間が存在する。それでもなお、この段階では時間は存在しない。次の段階として「素粒子が２つだけある宇宙空間」となると、互いの相互作用を記述する物理法則の意味が与えられる。ここに至って、記述のためのパラメータとして初めて時間が登場する。
　時間は、物理的に対象とすべき物理量ではなく、質量・空間・電荷などの物質属性の相互作用や運動を記述するための単位にすぎないのである。時間という概念は、まさしく“概念”の域を出ない。
　特殊相対性理論が絶対時間を否定し、各座標系に相対的に存在する“固有時” の概念を導いたのは特筆に値するが、それでも時間実存の呪縛からは解き放たれていない。それどころか、逆にミンコフスキー時空によって、時間は空間と同レベルの実存性を与えられてしまった。そして絶対時間を否定する代償として、今度は絶対的な速度、すなわち“光速度”を奉ることになったのである。この絶対視は100年もの間、神聖化され続けている。

　しかし人類は、アリストテレスの“重いものほど速く落下する”という概念の誤りに気づくのに2000年かかり、ニュートンの“絶対時間”という概念の誤りに気づくのに200年かかっている。神聖化された概念の誤りを改新することに、人類は多くの“時間”を必要としてきた。
　これらの歴史を思うとき、いつの日か人類は、絶対速度ｃと時間実存の誤謬に気づく時を必ずや迎えるであろうと、願わずにはいられないのである。

（以上）
1998年3月

表紙に戻る