表紙に戻る
階段のスイッチ
今回のテーマは「思索」というには少々大袈裟で、ちょっとした数理パズルの範疇かもしれません。
しかも今までのテーマと同様、周知の事実であり、私がその存在を知らなかっただけかもしれません。
しかし長年楽しみながら考え続け、先日ようやくとその解を得たので、ここにご披露したいと思います。
 階段を照らす電灯のスイッチが1階部分と2階部分の両方にあり、
そのどちらのスイッチからでも電灯のON/OFF制御が出来る事に、少年の頃いたく感激しました。
しかも信じられないほどシンプルな回路で、この制御を実現しているのです。
「世の中にはなんて知恵のある人がいるのだろう!」と、とても感心しました。
私はいつしか「3階建ての階段でも、この様なスイッチが作れないか」を考え始めました。
これが今回のテーマとなります。
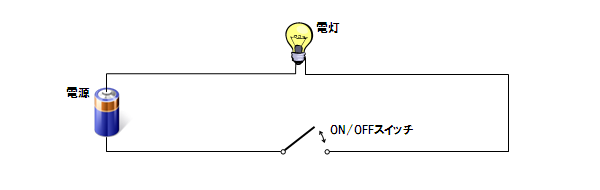
まず、この階段型のスイッチではない、一般のスイッチ回路を確認してみましょう。
果たしてこの回路をどの様に変形すれば、階段スイッチになるのでしょうか?
階段を照らす電灯のスイッチが1階部分と2階部分の両方にあり、
そのどちらのスイッチからでも電灯のON/OFF制御が出来る事に、少年の頃いたく感激しました。
しかも信じられないほどシンプルな回路で、この制御を実現しているのです。
「世の中にはなんて知恵のある人がいるのだろう!」と、とても感心しました。
私はいつしか「3階建ての階段でも、この様なスイッチが作れないか」を考え始めました。
これが今回のテーマとなります。
まず、この階段型のスイッチではない、一般のスイッチ回路を確認してみましょう。
果たしてこの回路をどの様に変形すれば、階段スイッチになるのでしょうか?
 実は、その仕組みは至って単純です。
1階と2階との間に2本の配線(A線とB線)を通し、各階にその切替スイッチを設けているだけです。
実は、その仕組みは至って単純です。
1階と2階との間に2本の配線(A線とB線)を通し、各階にその切替スイッチを設けているだけです。
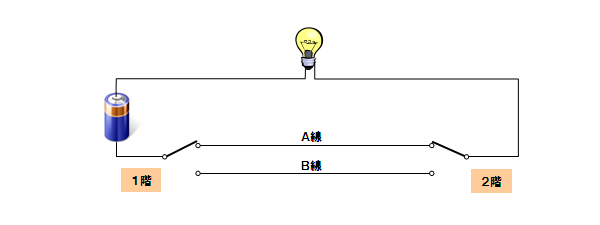 例えば、1階スイッチも2階スイッチもA線に導通する状態になっていれば照明が点灯します。
この状態で1階スイッチだけをB線側に切替えると消灯しますが、更にそこから2階スイッチも
B線側に切替えると、今度はB線を介して導通し再び点灯します。
単純でありながら極めて有効性の高い回路です。
素晴らしいですね。
建築用語として、この回路には名前が付いているであろうと推察していますが、
私はその名前すら知りません。
例えば、1階スイッチも2階スイッチもA線に導通する状態になっていれば照明が点灯します。
この状態で1階スイッチだけをB線側に切替えると消灯しますが、更にそこから2階スイッチも
B線側に切替えると、今度はB線を介して導通し再び点灯します。
単純でありながら極めて有効性の高い回路です。
素晴らしいですね。
建築用語として、この回路には名前が付いているであろうと推察していますが、
私はその名前すら知りません。
 では、これを3階、つまり3ヶ所から制御出来る様にするにはどうしたら良いのでしょうか?
一番初めに考えたのは、上記の回路に強引にもう一つのスイッチを挿入するイメージです。
このアイディアは2階だけが最大で4値のスイッチとなります。
多分2階のスイッチはダイヤル式となり、どこかに合わせれば点灯し、それ以外の所では消灯する
といったイメージになる事でしょう。
ダイヤル上の点灯/消灯の位置は、1階と3階の状態によって変化するため不定です。
でも4値ぐらいなら実用上耐えうるだろうと考えました。
では、これを3階、つまり3ヶ所から制御出来る様にするにはどうしたら良いのでしょうか?
一番初めに考えたのは、上記の回路に強引にもう一つのスイッチを挿入するイメージです。
このアイディアは2階だけが最大で4値のスイッチとなります。
多分2階のスイッチはダイヤル式となり、どこかに合わせれば点灯し、それ以外の所では消灯する
といったイメージになる事でしょう。
ダイヤル上の点灯/消灯の位置は、1階と3階の状態によって変化するため不定です。
でも4値ぐらいなら実用上耐えうるだろうと考えました。
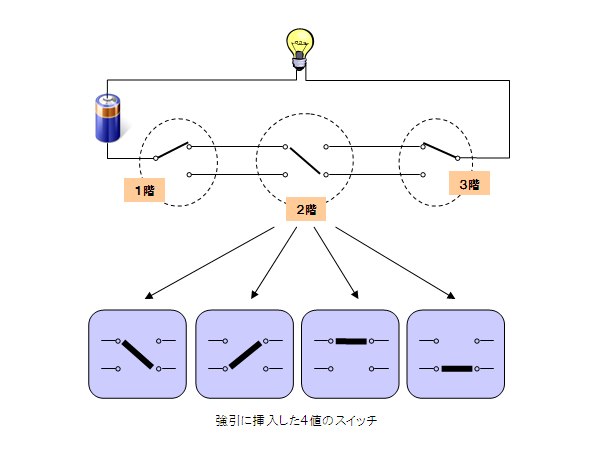 しかしこの回路がうまくいかないのは、すぐに判ります。
例えば上図は消灯状態ですが、1階のスイッチでこれを点灯状態にする事が出来ません。
まさに“浅知恵”“付け焼刃”の典型ですね(苦笑)。
別のアプローチも試してみました。各階を通す配線数を増やす方法です。
2階建ての時が2配線ですから、3階建ては3配線なのではないか・・・。
まあ、これが次の発想です。
しかしこの回路がうまくいかないのは、すぐに判ります。
例えば上図は消灯状態ですが、1階のスイッチでこれを点灯状態にする事が出来ません。
まさに“浅知恵”“付け焼刃”の典型ですね(苦笑)。
別のアプローチも試してみました。各階を通す配線数を増やす方法です。
2階建ての時が2配線ですから、3階建ては3配線なのではないか・・・。
まあ、これが次の発想です。
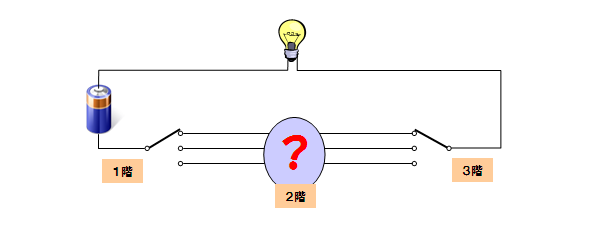 これだと1階と3階のスイッチは3値になってしまいますし、
2階のスイッチに至っては最大で9値になってしまいます。
そして、この方式でもうまく制御できない例はすぐに見つかりました。
そもそもこれらのアプローチは「美しさ」という観点からして、
次第に正解から遠ざかっている気さえします。
これだと1階と3階のスイッチは3値になってしまいますし、
2階のスイッチに至っては最大で9値になってしまいます。
そして、この方式でもうまく制御できない例はすぐに見つかりました。
そもそもこれらのアプローチは「美しさ」という観点からして、
次第に正解から遠ざかっている気さえします。
 その後もいろいろな代案を考えたのですが、なかなかうまくいかずに月日が経って行きました。
まあ納期があるわけでもないので、手持ち無沙汰な時間に頭の中でちょっと考えてみる、
といった程度の極めて断続的な楽しみ方をしていたのですが・・・。
そして最近、ボケ防止も兼ねて(笑)、ちょっと本腰を入れて考えてみる事にしたのです。
しかし今までのように思い付きで無作為に試してもそう簡単に解決できる程
生易しいパズルではないという事に気づきました。
何らかの戦略的な指針が必要なのです。
そこで、まず考えた事は以下の様な指針でした。
もし、3階建てへの拡張に留まらず、
n階建てのスイッチにも拡張できる可能性があるならば、
このパズルの解答は、必ずや「美しい対称性」を持っているはずだ。
それを実現するためには各階のスイッチは対等の構造を持つべきであり、
よって、各スイッチは複数の配線同士の接続関係を切替えるタイプになるだろう、
と考えました。
また、ONとOFFで対称構造を維持するためには、
各階のスイッチは2値や4値といった偶数値であるべきで、
もっともシンプルで美しい解として、まずは2値を採択すべきと考えました。
また、同様の理由から配線数も偶数でなければならいとも考えました。
2階建ての2本に対して、次の偶数は4本です。
そこで、3階建ての階段スイッチには最低でも4配線が必要だという仮説を立てました。
その後もいろいろな代案を考えたのですが、なかなかうまくいかずに月日が経って行きました。
まあ納期があるわけでもないので、手持ち無沙汰な時間に頭の中でちょっと考えてみる、
といった程度の極めて断続的な楽しみ方をしていたのですが・・・。
そして最近、ボケ防止も兼ねて(笑)、ちょっと本腰を入れて考えてみる事にしたのです。
しかし今までのように思い付きで無作為に試してもそう簡単に解決できる程
生易しいパズルではないという事に気づきました。
何らかの戦略的な指針が必要なのです。
そこで、まず考えた事は以下の様な指針でした。
もし、3階建てへの拡張に留まらず、
n階建てのスイッチにも拡張できる可能性があるならば、
このパズルの解答は、必ずや「美しい対称性」を持っているはずだ。
それを実現するためには各階のスイッチは対等の構造を持つべきであり、
よって、各スイッチは複数の配線同士の接続関係を切替えるタイプになるだろう、
と考えました。
また、ONとOFFで対称構造を維持するためには、
各階のスイッチは2値や4値といった偶数値であるべきで、
もっともシンプルで美しい解として、まずは2値を採択すべきと考えました。
また、同様の理由から配線数も偶数でなければならいとも考えました。
2階建ての2本に対して、次の偶数は4本です。
そこで、3階建ての階段スイッチには最低でも4配線が必要だという仮説を立てました。
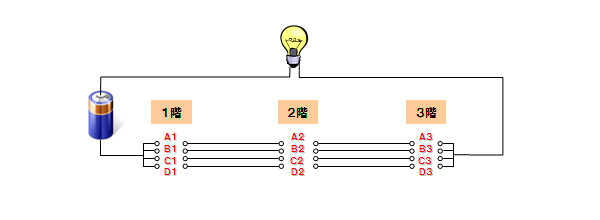 3階建ての4本配線において、2値のスイッチで対称性を維持するために、
各階のスイッチは、2配線を接続し他の2配線を断線する、という構造になっているはずです。
つまり、スイッチの切替えで2配線が入れ替わるという対称構造を仮定しました。
この条件下で、各階のスイッチが互いに補間し合う様なパターンを模索すれば良いのです。
この指針を元に試行錯誤した結果、ついに解を見つける事が出来ました!
以下がそのスイッチ構造です。
3階建ての4本配線において、2値のスイッチで対称性を維持するために、
各階のスイッチは、2配線を接続し他の2配線を断線する、という構造になっているはずです。
つまり、スイッチの切替えで2配線が入れ替わるという対称構造を仮定しました。
この条件下で、各階のスイッチが互いに補間し合う様なパターンを模索すれば良いのです。
この指針を元に試行錯誤した結果、ついに解を見つける事が出来ました!
以下がそのスイッチ構造です。
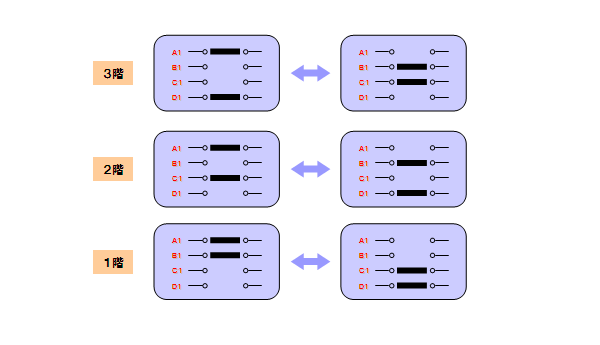 このパターンでスイッチを組み合わせれば、他の階がどの様な状態になっていても
対象とする階の切替えで照明のON/OFFを制御できます。
しかもどの階のスイッチも2値ですから、
利用者からすれば2階建てのスイッチと同様の操作感や外観を持ちます。
各階を結ぶ配線が4本に増えますが、それほどのコストアップにならないでしょう。
実用性も充分にあると思えます。
しかし実用性うんぬんよりも、その美しい対称性に満足感を感じます。
対称性が満たされているため、各階のスイッチの構造も共通化できる事も思い付きました。
例えば、以下の図のようにT字型のレバーを用意してT字の中程に支点を設けます。
つまみを左に動かすと、右側の2つの端子を上下に接続し、左側の上下2つの端子を開放します。
このパターンでスイッチを組み合わせれば、他の階がどの様な状態になっていても
対象とする階の切替えで照明のON/OFFを制御できます。
しかもどの階のスイッチも2値ですから、
利用者からすれば2階建てのスイッチと同様の操作感や外観を持ちます。
各階を結ぶ配線が4本に増えますが、それほどのコストアップにならないでしょう。
実用性も充分にあると思えます。
しかし実用性うんぬんよりも、その美しい対称性に満足感を感じます。
対称性が満たされているため、各階のスイッチの構造も共通化できる事も思い付きました。
例えば、以下の図のようにT字型のレバーを用意してT字の中程に支点を設けます。
つまみを左に動かすと、右側の2つの端子を上下に接続し、左側の上下2つの端子を開放します。
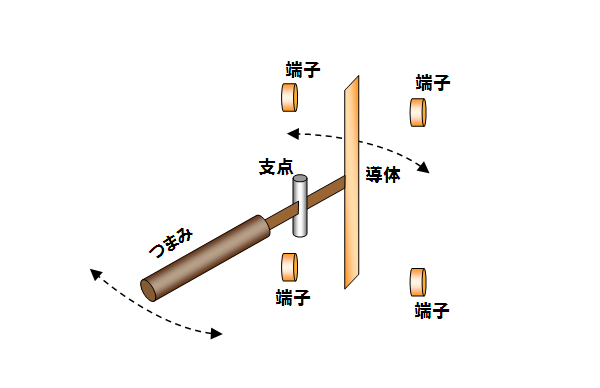 このようなスイッチがあれば、配線の接続の仕方だけで各階のパターンを実現できます。
例えば、
1階は左側端子にA線とB線を接続し、右側端子にC線とD線をつなぎます。
2階は左側端子にA線とC線を接続し、右側端子にB線とD線をつなぎます。
このようなスイッチがあれば、配線の接続の仕方だけで各階のパターンを実現できます。
例えば、
1階は左側端子にA線とB線を接続し、右側端子にC線とD線をつなぎます。
2階は左側端子にA線とC線を接続し、右側端子にB線とD線をつなぎます。
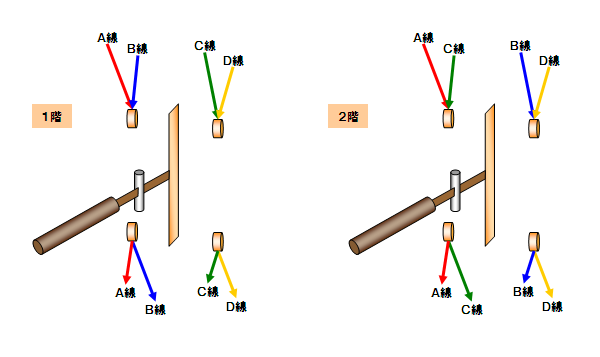 むろん、3階の接続も同様な方法で実現できます。
一々、各階用のスイッチを製作する必要は無いのです。
美しい設計はハードウェアの無駄も取り除く、という典型的な例だと思います。
むろん、3階の接続も同様な方法で実現できます。
一々、各階用のスイッチを製作する必要は無いのです。
美しい設計はハードウェアの無駄も取り除く、という典型的な例だと思います。
 さてこれで当初設定した“パズル”は一応解けました。
しかし“パズル”を“思索”に昇華させるには、ここで終わらせてはいけません。
実はここから思索としては面白く美味しいプロセスなのです。
アルキメデスを例に挙げるのはおこがましいのですが、彼が風呂に体を沈めた時、
湯船から溢れるお湯を見て王冠の体積を測定する方法を思い付いた瞬間が
“パズル”を解いたポイントとすれば、更にそこから浮力の法則を導き出すプロセスこそが
“思索”の領域と言えるでしょう。
「王冠」の方は多分納期があったでしょうが、「浮力」の方は無かったはずです。
思索への取っ掛かりとして3階建ての階段スイッチの解を4階建てに拡張する事を試み、
その拡張過程で背後に存在するであろうより普遍的なものを感じ取って見ようと思いました。
その副次成果として、n階建てへの拡張方式も得られるはずです。
まず、3階建ての階段スイッチで用いた4配線を、正方形の頂点(A,B,C,D)として配置します。
そして、各階のスイッチパターンがどの様になるかを確認します。
幾何的なアプローチにより、背後に潜む美しい何かが見えてくるのではないかと思ったのです。
その効能は直ぐに現れました。
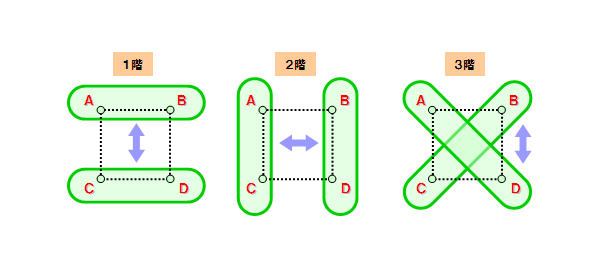
1階と2階は互いに向かい合う辺を、上下もしくは左右に切替えるパターンである事が判ります。
そして3階は、2つある対角線を切替えるパターンになっています。
なかなか美しい関係が見えてきました。
2つ頂点の組合せを切替える方法は、これ以外にありません。唯一無二のセットです。
さてこれで当初設定した“パズル”は一応解けました。
しかし“パズル”を“思索”に昇華させるには、ここで終わらせてはいけません。
実はここから思索としては面白く美味しいプロセスなのです。
アルキメデスを例に挙げるのはおこがましいのですが、彼が風呂に体を沈めた時、
湯船から溢れるお湯を見て王冠の体積を測定する方法を思い付いた瞬間が
“パズル”を解いたポイントとすれば、更にそこから浮力の法則を導き出すプロセスこそが
“思索”の領域と言えるでしょう。
「王冠」の方は多分納期があったでしょうが、「浮力」の方は無かったはずです。
思索への取っ掛かりとして3階建ての階段スイッチの解を4階建てに拡張する事を試み、
その拡張過程で背後に存在するであろうより普遍的なものを感じ取って見ようと思いました。
その副次成果として、n階建てへの拡張方式も得られるはずです。
まず、3階建ての階段スイッチで用いた4配線を、正方形の頂点(A,B,C,D)として配置します。
そして、各階のスイッチパターンがどの様になるかを確認します。
幾何的なアプローチにより、背後に潜む美しい何かが見えてくるのではないかと思ったのです。
その効能は直ぐに現れました。
1階と2階は互いに向かい合う辺を、上下もしくは左右に切替えるパターンである事が判ります。
そして3階は、2つある対角線を切替えるパターンになっています。
なかなか美しい関係が見えてきました。
2つ頂点の組合せを切替える方法は、これ以外にありません。唯一無二のセットです。
 では4階建ての場合は、この美しい対称性をどの様に拡張すれば良いのでしょうか?
論理的アプローチではなく、美的アプローチで試してみました。
すなわち3階建てと同様の対称性が保たれるはずであるという仮説です。
指針では、配線数は偶数であると仮定していました。
そして、3階建てでの4本配線は唯一無二に充足しているため、
4階建てはそれよりも多い配線が必要なはずです。つまり、次の偶数6本となります。
そこで3階建ての時と同様に、六角形の頂点を配線経路と見なして
いろいろと試行錯誤をしたのですが、6本ではなかなかうまくいきませんでした。
そこで、次の配線数を試みる事にしました。つまり8本です。
そして8本ともなると、八角形よりももっと魅力的な
幾何イメージの飛躍が可能である事に気づきました。
3階建ての「正方形」に対し、4階建ては「立方体」を構築できるのです。
つまり、2次元から3次元に拡張される訳です。
そして、スイッチの切替えパターンの組み合わせは、
3階建てが「辺」だった事から、4階建ては「面」になるだろうと予測できます。
では4階建ての場合は、この美しい対称性をどの様に拡張すれば良いのでしょうか?
論理的アプローチではなく、美的アプローチで試してみました。
すなわち3階建てと同様の対称性が保たれるはずであるという仮説です。
指針では、配線数は偶数であると仮定していました。
そして、3階建てでの4本配線は唯一無二に充足しているため、
4階建てはそれよりも多い配線が必要なはずです。つまり、次の偶数6本となります。
そこで3階建ての時と同様に、六角形の頂点を配線経路と見なして
いろいろと試行錯誤をしたのですが、6本ではなかなかうまくいきませんでした。
そこで、次の配線数を試みる事にしました。つまり8本です。
そして8本ともなると、八角形よりももっと魅力的な
幾何イメージの飛躍が可能である事に気づきました。
3階建ての「正方形」に対し、4階建ては「立方体」を構築できるのです。
つまり、2次元から3次元に拡張される訳です。
そして、スイッチの切替えパターンの組み合わせは、
3階建てが「辺」だった事から、4階建ては「面」になるだろうと予測できます。
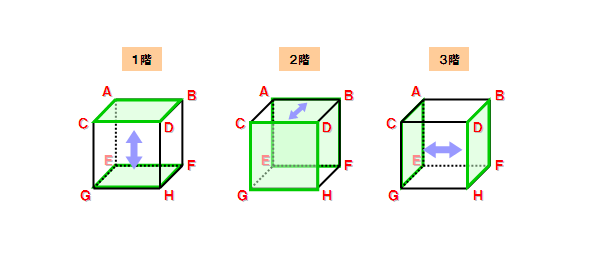 さて、問題は4階部分の切替えスイッチのパターンです。3階建てでは「対角線」でした。
しかし立方体の対角線は4本あるため、対称性が崩れます。
対称性を実現するためには共役関係が成り立っている必要があると直感しました。
しかも、4階建てのパターンは4つの頂点から構築される必要がありますが、
単純な対角線ではその端点である2つの頂点しか含まれません。
2値の切替えつまり共役性を満たし、4頂点を含む描像は如何なるものになるでしょうか?
見つけました!
それが、下記の図になります。
さて、問題は4階部分の切替えスイッチのパターンです。3階建てでは「対角線」でした。
しかし立方体の対角線は4本あるため、対称性が崩れます。
対称性を実現するためには共役関係が成り立っている必要があると直感しました。
しかも、4階建てのパターンは4つの頂点から構築される必要がありますが、
単純な対角線ではその端点である2つの頂点しか含まれません。
2値の切替えつまり共役性を満たし、4頂点を含む描像は如何なるものになるでしょうか?
見つけました!
それが、下記の図になります。
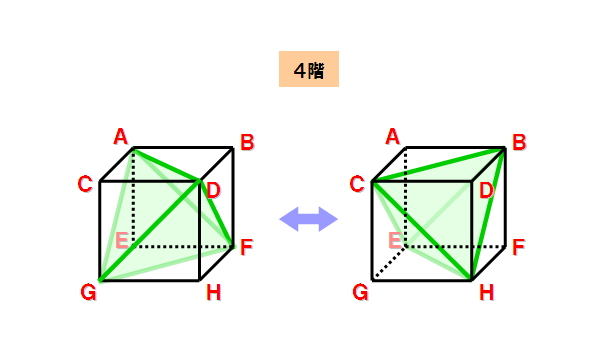 これは立方体の内側に存在する立体で、よく見ると正四面体となっています。
しかも立方体の中にはこの2つしか存在せず、共役性を満たしながら解が一意に決まります。
私はこれを、立方体の「対角面」と名付けたいと思います。
まさに、正方形の「対角線」の拡張です。
今回の思索テーマは階段スイッチの拡張であった訳ですが、
図らずも対角線の次元を1つ上げた描像を得た事になります。
なんと美しい形状でしょうか!
★ 正直、この双対な「対角面」の発見が、今回の思索の中で最も興奮した瞬間でした!
さて、階段スイッチのテーマに戻しましょう。
以上で得た4階建ての階段スイッチを、そのパターンとして描くと以下のようになります。
これは立方体の内側に存在する立体で、よく見ると正四面体となっています。
しかも立方体の中にはこの2つしか存在せず、共役性を満たしながら解が一意に決まります。
私はこれを、立方体の「対角面」と名付けたいと思います。
まさに、正方形の「対角線」の拡張です。
今回の思索テーマは階段スイッチの拡張であった訳ですが、
図らずも対角線の次元を1つ上げた描像を得た事になります。
なんと美しい形状でしょうか!
★ 正直、この双対な「対角面」の発見が、今回の思索の中で最も興奮した瞬間でした!
さて、階段スイッチのテーマに戻しましょう。
以上で得た4階建ての階段スイッチを、そのパターンとして描くと以下のようになります。
 大変複雑そうでボリューム感のある結果となりました。
しかしここでも各階スイッチは2値であり、しかも前述のT字スイッチがそのまま利用できます!
各端子に接続される配線が2本から4本に増えるだけです。
実際にこのパターンが目的を達成しているかどうかを確認するために、
簡単なプログラムを作って、あらゆる状態からON/OFF操作が出来る事も確認しました。
計算機は問題を解くことは苦手ですが、成否を検証するのは得意ですね(笑)。
大変複雑そうでボリューム感のある結果となりました。
しかしここでも各階スイッチは2値であり、しかも前述のT字スイッチがそのまま利用できます!
各端子に接続される配線が2本から4本に増えるだけです。
実際にこのパターンが目的を達成しているかどうかを確認するために、
簡単なプログラムを作って、あらゆる状態からON/OFF操作が出来る事も確認しました。
計算機は問題を解くことは苦手ですが、成否を検証するのは得意ですね(笑)。
 さて、2階建ての階段スイッチを3階建て、4階建てへと進めてきました。
その手法は対称性をベースにした類推と、幾何的な考察が中心でした。
幾何的な考察は直感的であり状態の把握も容易なのですが、いかんせん拡張は3次元空間までです。
n階建てに駒を進めるには、論理学か代数的なアプローチに方針を変更するしかありません。
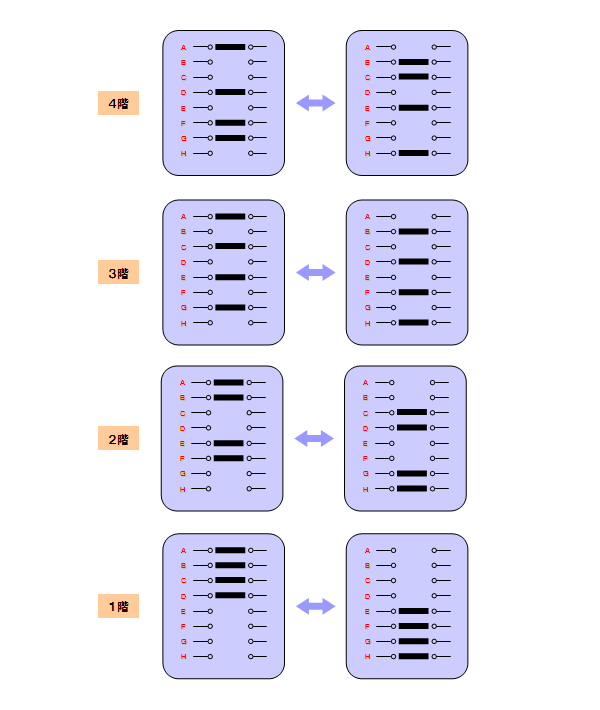
そこで4階建ての階段スイッチの解を以下のように書き表し、その規則性を考察してみる事にします。
さて、2階建ての階段スイッチを3階建て、4階建てへと進めてきました。
その手法は対称性をベースにした類推と、幾何的な考察が中心でした。
幾何的な考察は直感的であり状態の把握も容易なのですが、いかんせん拡張は3次元空間までです。
n階建てに駒を進めるには、論理学か代数的なアプローチに方針を変更するしかありません。
そこで4階建ての階段スイッチの解を以下のように書き表し、その規則性を考察してみる事にします。
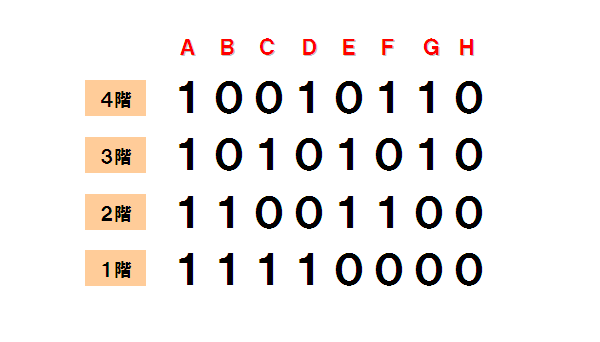 一種のマトリックスです。
左から右に各配線経路(A,B,C,・・・)を並べ、下から上に各階を積上げます。
すなわち、各列は全階を貫く配線を表し、各行はその階のスイッチを表します。
各欄にはスイッチの状態として、1で導通を、0で断線を表わす様に数値を与えておきます。
2階のスイッチを切替える操作は、2階の行の1と0を全て反転させる事に相当します。
照明が着いているのか消えているのかは、以下のルールで状態確認をすれば判断できます。
・少なくとも一つの配線経路で、すべて“1”となっていれば点灯
・すべての配線経路で、少なくとも一つの“0”があれば消灯
一種のマトリックスです。
左から右に各配線経路(A,B,C,・・・)を並べ、下から上に各階を積上げます。
すなわち、各列は全階を貫く配線を表し、各行はその階のスイッチを表します。
各欄にはスイッチの状態として、1で導通を、0で断線を表わす様に数値を与えておきます。
2階のスイッチを切替える操作は、2階の行の1と0を全て反転させる事に相当します。
照明が着いているのか消えているのかは、以下のルールで状態確認をすれば判断できます。
・少なくとも一つの配線経路で、すべて“1”となっていれば点灯
・すべての配線経路で、少なくとも一つの“0”があれば消灯
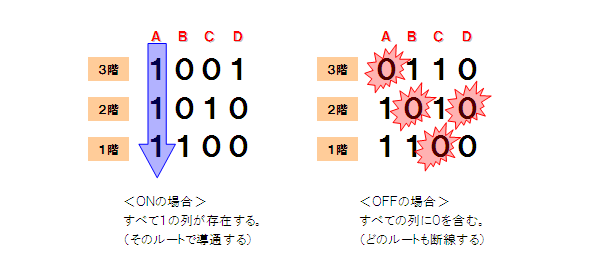 階段スイッチのパズルとは、結局このマトリックスを導き出す事にあります。
既に得られてる3階建てのマトリックスから、4階建てのマトリックスを導く方法を考えてみましょう。
(1)まず3階建てマトリックス(これは4×4行列)を点灯状態にしておきます。
→これを点灯ブロックと呼びます。
(2)そして消灯状態マトリックス(これも4×4行列)も用意します。
→これを消灯ブロックと呼びます。
※点灯(1)から消灯(2)へと状態を変えるには、
どこか1つの階のスイッチを反転(切替え)すればすぐに得る事が出来ます。
(3)この点灯ブロックと消灯ブロックを横に並べ、1階部分に新しいスイッチ(行)を挿入します。
その新しい行の各列の値はとても単純なルールで与えます。
そのルールとは、「点灯ブロック直下は1、消灯ブロックの直下は0」です。
これで4階建てのマトリックスが出来上がります。
階段スイッチのパズルとは、結局このマトリックスを導き出す事にあります。
既に得られてる3階建てのマトリックスから、4階建てのマトリックスを導く方法を考えてみましょう。
(1)まず3階建てマトリックス(これは4×4行列)を点灯状態にしておきます。
→これを点灯ブロックと呼びます。
(2)そして消灯状態マトリックス(これも4×4行列)も用意します。
→これを消灯ブロックと呼びます。
※点灯(1)から消灯(2)へと状態を変えるには、
どこか1つの階のスイッチを反転(切替え)すればすぐに得る事が出来ます。
(3)この点灯ブロックと消灯ブロックを横に並べ、1階部分に新しいスイッチ(行)を挿入します。
その新しい行の各列の値はとても単純なルールで与えます。
そのルールとは、「点灯ブロック直下は1、消灯ブロックの直下は0」です。
これで4階建てのマトリックスが出来上がります。
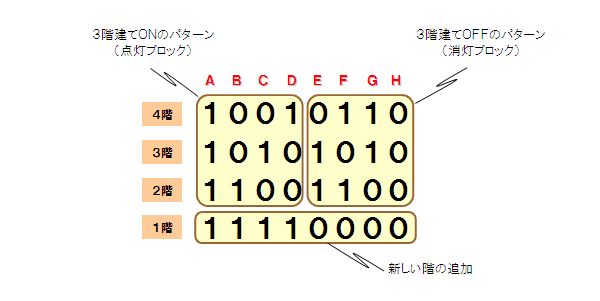 以上は3階建てから4階建てを導く手順ですが、
この手続きは「n階建て」から「n+1階建て」を導く一般的な方法として成り立ちます。
実は、新しく挿入する行は1階である必要は無く、どの階の位置でも問題はありませんし、
その挿入した行の値は「点灯ブロック直下が0で、消灯ブロック直下が1」でも構いません。
(照明の初期状態が、点灯なのか消灯なのかが変わるだけです)
この手続きの論理的な背景は、以下に寄ります。
以上は3階建てから4階建てを導く手順ですが、
この手続きは「n階建て」から「n+1階建て」を導く一般的な方法として成り立ちます。
実は、新しく挿入する行は1階である必要は無く、どの階の位置でも問題はありませんし、
その挿入した行の値は「点灯ブロック直下が0で、消灯ブロック直下が1」でも構いません。
(照明の初期状態が、点灯なのか消灯なのかが変わるだけです)
この手続きの論理的な背景は、以下に寄ります。
新しく追加した階のスイッチは、
点灯ブロックと消灯ブロックという2つの世界を切替える意味を持ち、
このスイッチが固定であれば、一つ少ない階数建てを制御している事と同値である。
一方、点灯ブロックと消灯ブロックはスイッチを切替えるたびに、
ブロック単位に点灯と消灯の状態が反転するため、
最後に加えた階のスイッチを切替える事で、ON/OFF制御が効くようになる。
|
この論理的な考察が正しく、解を導く手続きが間違っていないかどうか、
既に解を得ている3階建てや2階建てのマトリックスで検証してみましょう。
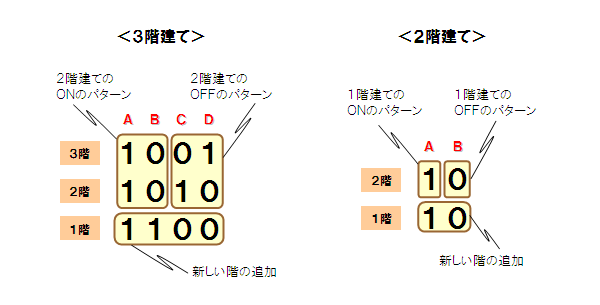 どうやら正しく機能しているようです。
以上の手続きの論理的帰結として、
n階建ての階段スイッチには、2の(n-1)乗の配線が必要
という規則が導けます。
どうやら正しく機能しているようです。
以上の手続きの論理的帰結として、
n階建ての階段スイッチには、2の(n-1)乗の配線が必要
という規則が導けます。
 比較的簡単な手順で何階建てでも解を得られる事が判ったので、
6階建てのマトリックスを描いてみました。
配線は32本にもなりますが、ルールは単純なので簡単です。
そして、このマトリックスを描く過程で、
各階に割り当てるスイッチ配列を整理していたら、更に見通しが良くなる事に気づきました。
比較的簡単な手順で何階建てでも解を得られる事が判ったので、
6階建てのマトリックスを描いてみました。
配線は32本にもなりますが、ルールは単純なので簡単です。
そして、このマトリックスを描く過程で、
各階に割り当てるスイッチ配列を整理していたら、更に見通しが良くなる事に気づきました。
 1階は、1と0が交互に並ぶパターン。
2階は、1が2回、0が2回と繰り返すパターン。
3階は、1が4回、0が4回と繰り返すパターン。
・・・
といった感じです。
結局、nを対象とする階数とすると、
各階のスイッチパターンは、2の(n-1)乗の周期で1と0を繰り返せば良い事になります。
しかるに、最上階だけは周期が乱れます。
最上階は、点灯ブロックと消灯ブロックの分離を一身に背負っており、
反転してコピーする過程を繰り返すために、結果として周期を見出せないパターンになるのです。
1階は、1と0が交互に並ぶパターン。
2階は、1が2回、0が2回と繰り返すパターン。
3階は、1が4回、0が4回と繰り返すパターン。
・・・
といった感じです。
結局、nを対象とする階数とすると、
各階のスイッチパターンは、2の(n-1)乗の周期で1と0を繰り返せば良い事になります。
しかるに、最上階だけは周期が乱れます。
最上階は、点灯ブロックと消灯ブロックの分離を一身に背負っており、
反転してコピーする過程を繰り返すために、結果として周期を見出せないパターンになるのです。
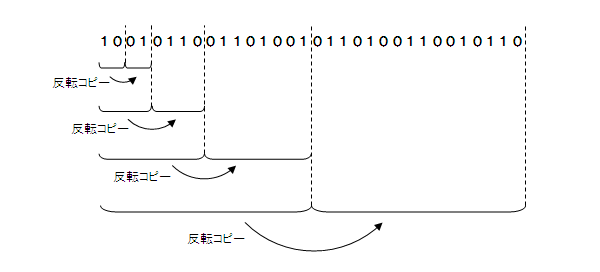 しかし、この最上階の1と0の並びを注意深く観察してみると、
反転コピー方式で解を得る以外に、もう一つ別のやり方がある事に気づきました。
この新しい方式の方が、計算をアルゴリズム化したり、数式化するに有利かもしれません。
まず、1は「1と0」に、0は「0と1」に“増殖”するという基本ルールを設定します。
しかし、この最上階の1と0の並びを注意深く観察してみると、
反転コピー方式で解を得る以外に、もう一つ別のやり方がある事に気づきました。
この新しい方式の方が、計算をアルゴリズム化したり、数式化するに有利かもしれません。
まず、1は「1と0」に、0は「0と1」に“増殖”するという基本ルールを設定します。
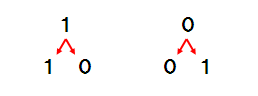 そして、ただ一つの1を“種”として階層的な増殖プロセスを開始します。
その様子を示したのが次の図です。
そして、ただ一つの1を“種”として階層的な増殖プロセスを開始します。
その様子を示したのが次の図です。
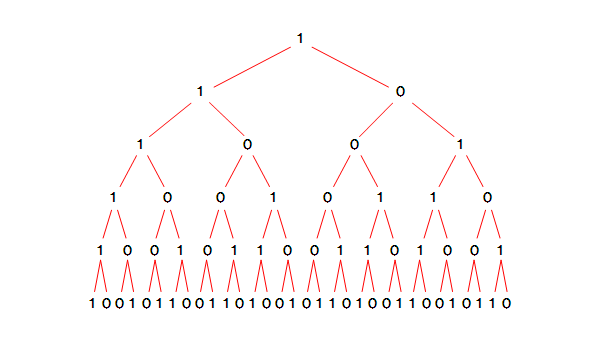 いかがでしょうか。
図の最後の階層には6階建てにおける最上階スイッチパターンが現れているのが判ると思います。
実はこの階層図は、各階層がそれぞれの階数の最上階スイッチパターンに符合しているのです。
この階層図は、よくよく眺めていると面白い性質を持っている事が判ります。
どのノードから始めても、左側に降りて行く階層は全体と部分が一致しています。
逆に、右側に降りて行く階層は全体と部分が正反対の値を持っているのです。
まるで、フラクタルと反フラクタルがハイブリッドになっているような構造ですね。
いかがでしょうか。
図の最後の階層には6階建てにおける最上階スイッチパターンが現れているのが判ると思います。
実はこの階層図は、各階層がそれぞれの階数の最上階スイッチパターンに符合しているのです。
この階層図は、よくよく眺めていると面白い性質を持っている事が判ります。
どのノードから始めても、左側に降りて行く階層は全体と部分が一致しています。
逆に、右側に降りて行く階層は全体と部分が正反対の値を持っているのです。
まるで、フラクタルと反フラクタルがハイブリッドになっているような構造ですね。
 2階建ての階段のスイッチが、
実にシンプルな回路で鮮やかな制御をしているという驚きに端を発して、
最後は、このように面白く不思議な階層図に達する事が出来ました。
この階層構造がどんな意味を持っているか、今のところ私にも判りません。
ただ、愉快なイメージは膨らむのです。
今、この宇宙空間全体が無数のスイッチで埋められていて、
それらは隣り合うスイッチにだけ接続されているとします。まあ、一種の近接作用ですね。
にも関わらず、どのスイッチを局所的に切替えても全体に影響を与える制御ができるのです。
その制御を可能にする条件は、
「極めて周期性の高いパターンと、不思議な階層を持つパターンで構成される」
という事を示唆しているのかもしれません。
何か深遠なものを感じさせる今回の思索の旅でした。
2階建ての階段のスイッチが、
実にシンプルな回路で鮮やかな制御をしているという驚きに端を発して、
最後は、このように面白く不思議な階層図に達する事が出来ました。
この階層構造がどんな意味を持っているか、今のところ私にも判りません。
ただ、愉快なイメージは膨らむのです。
今、この宇宙空間全体が無数のスイッチで埋められていて、
それらは隣り合うスイッチにだけ接続されているとします。まあ、一種の近接作用ですね。
にも関わらず、どのスイッチを局所的に切替えても全体に影響を与える制御ができるのです。
その制御を可能にする条件は、
「極めて周期性の高いパターンと、不思議な階層を持つパターンで構成される」
という事を示唆しているのかもしれません。
何か深遠なものを感じさせる今回の思索の旅でした。
 (2011.09.17追記)
上記の様な考察を綿々と綴ってきましたが、昨日匿名の方から以下のメールを頂きました。
やはりこの命題は既知のものであり、しかももっとエレガントな解法が存在していました。
情報のご提供ありがとうございました。
●3路・4路スイッチ
なんと、どの様な階数であろうとも2本の配線で階段のスイッチを実現しています。
実に鮮やかです!
2階の階段スイッチは「3路スイッチ」と呼ばれ、
更にどの階数でも可能とするためのスイッチは「4路スイッチ」と呼ばれているそうです。
しっかりと名称が与えられているということは、既に業界では常識化されているという事ですね。
特筆すべきは、上記の解法は3路スイッチと4路スイッチの組合せになっているという事です。
1階と最上階は3路スイッチを、間の階は4路スイッチを使用しています。
私が解を得ようとする過程で「対称性」という方針を打ち立てた時点で、
この4路スイッチとは別の方向に進んでしまったようです。
私の到達した方式でも問題は解決するのですが、階が増すごとに配線が指数的に増え実用的ではない。
それに比べて4路スイッチのエレガントさは、見事としか言い様がありません。
私はひどく遠回りしていたどころか、最終的な“階”いや“解”に到達できなかったみたいです。orz
でも逆に“サイト検索”に頼らず最後まで自分の力で考え抜こう、という姿勢で
私が思索に臨んでいる事は示せたかもしれませんね・・・(苦笑)
(2011.09.17追記)
上記の様な考察を綿々と綴ってきましたが、昨日匿名の方から以下のメールを頂きました。
やはりこの命題は既知のものであり、しかももっとエレガントな解法が存在していました。
情報のご提供ありがとうございました。
●3路・4路スイッチ
なんと、どの様な階数であろうとも2本の配線で階段のスイッチを実現しています。
実に鮮やかです!
2階の階段スイッチは「3路スイッチ」と呼ばれ、
更にどの階数でも可能とするためのスイッチは「4路スイッチ」と呼ばれているそうです。
しっかりと名称が与えられているということは、既に業界では常識化されているという事ですね。
特筆すべきは、上記の解法は3路スイッチと4路スイッチの組合せになっているという事です。
1階と最上階は3路スイッチを、間の階は4路スイッチを使用しています。
私が解を得ようとする過程で「対称性」という方針を打ち立てた時点で、
この4路スイッチとは別の方向に進んでしまったようです。
私の到達した方式でも問題は解決するのですが、階が増すごとに配線が指数的に増え実用的ではない。
それに比べて4路スイッチのエレガントさは、見事としか言い様がありません。
私はひどく遠回りしていたどころか、最終的な“階”いや“解”に到達できなかったみたいです。orz
でも逆に“サイト検索”に頼らず最後まで自分の力で考え抜こう、という姿勢で
私が思索に臨んでいる事は示せたかもしれませんね・・・(苦笑)
表紙に戻る
 階段を照らす電灯のスイッチが1階部分と2階部分の両方にあり、
そのどちらのスイッチからでも電灯のON/OFF制御が出来る事に、少年の頃いたく感激しました。
しかも信じられないほどシンプルな回路で、この制御を実現しているのです。
「世の中にはなんて知恵のある人がいるのだろう!」と、とても感心しました。
私はいつしか「3階建ての階段でも、この様なスイッチが作れないか」を考え始めました。
これが今回のテーマとなります。
まず、この階段型のスイッチではない、一般のスイッチ回路を確認してみましょう。
果たしてこの回路をどの様に変形すれば、階段スイッチになるのでしょうか?
階段を照らす電灯のスイッチが1階部分と2階部分の両方にあり、
そのどちらのスイッチからでも電灯のON/OFF制御が出来る事に、少年の頃いたく感激しました。
しかも信じられないほどシンプルな回路で、この制御を実現しているのです。
「世の中にはなんて知恵のある人がいるのだろう!」と、とても感心しました。
私はいつしか「3階建ての階段でも、この様なスイッチが作れないか」を考え始めました。
これが今回のテーマとなります。
まず、この階段型のスイッチではない、一般のスイッチ回路を確認してみましょう。
果たしてこの回路をどの様に変形すれば、階段スイッチになるのでしょうか?
 実は、その仕組みは至って単純です。
1階と2階との間に2本の配線(A線とB線)を通し、各階にその切替スイッチを設けているだけです。
実は、その仕組みは至って単純です。
1階と2階との間に2本の配線(A線とB線)を通し、各階にその切替スイッチを設けているだけです。
 例えば、1階スイッチも2階スイッチもA線に導通する状態になっていれば照明が点灯します。
この状態で1階スイッチだけをB線側に切替えると消灯しますが、更にそこから2階スイッチも
B線側に切替えると、今度はB線を介して導通し再び点灯します。
単純でありながら極めて有効性の高い回路です。
素晴らしいですね。
建築用語として、この回路には名前が付いているであろうと推察していますが、
私はその名前すら知りません。
例えば、1階スイッチも2階スイッチもA線に導通する状態になっていれば照明が点灯します。
この状態で1階スイッチだけをB線側に切替えると消灯しますが、更にそこから2階スイッチも
B線側に切替えると、今度はB線を介して導通し再び点灯します。
単純でありながら極めて有効性の高い回路です。
素晴らしいですね。
建築用語として、この回路には名前が付いているであろうと推察していますが、
私はその名前すら知りません。
 では、これを3階、つまり3ヶ所から制御出来る様にするにはどうしたら良いのでしょうか?
一番初めに考えたのは、上記の回路に強引にもう一つのスイッチを挿入するイメージです。
このアイディアは2階だけが最大で4値のスイッチとなります。
多分2階のスイッチはダイヤル式となり、どこかに合わせれば点灯し、それ以外の所では消灯する
といったイメージになる事でしょう。
ダイヤル上の点灯/消灯の位置は、1階と3階の状態によって変化するため不定です。
でも4値ぐらいなら実用上耐えうるだろうと考えました。
では、これを3階、つまり3ヶ所から制御出来る様にするにはどうしたら良いのでしょうか?
一番初めに考えたのは、上記の回路に強引にもう一つのスイッチを挿入するイメージです。
このアイディアは2階だけが最大で4値のスイッチとなります。
多分2階のスイッチはダイヤル式となり、どこかに合わせれば点灯し、それ以外の所では消灯する
といったイメージになる事でしょう。
ダイヤル上の点灯/消灯の位置は、1階と3階の状態によって変化するため不定です。
でも4値ぐらいなら実用上耐えうるだろうと考えました。
 しかしこの回路がうまくいかないのは、すぐに判ります。
例えば上図は消灯状態ですが、1階のスイッチでこれを点灯状態にする事が出来ません。
まさに“浅知恵”“付け焼刃”の典型ですね(苦笑)。
別のアプローチも試してみました。各階を通す配線数を増やす方法です。
2階建ての時が2配線ですから、3階建ては3配線なのではないか・・・。
まあ、これが次の発想です。
しかしこの回路がうまくいかないのは、すぐに判ります。
例えば上図は消灯状態ですが、1階のスイッチでこれを点灯状態にする事が出来ません。
まさに“浅知恵”“付け焼刃”の典型ですね(苦笑)。
別のアプローチも試してみました。各階を通す配線数を増やす方法です。
2階建ての時が2配線ですから、3階建ては3配線なのではないか・・・。
まあ、これが次の発想です。
 これだと1階と3階のスイッチは3値になってしまいますし、
2階のスイッチに至っては最大で9値になってしまいます。
そして、この方式でもうまく制御できない例はすぐに見つかりました。
そもそもこれらのアプローチは「美しさ」という観点からして、
次第に正解から遠ざかっている気さえします。
これだと1階と3階のスイッチは3値になってしまいますし、
2階のスイッチに至っては最大で9値になってしまいます。
そして、この方式でもうまく制御できない例はすぐに見つかりました。
そもそもこれらのアプローチは「美しさ」という観点からして、
次第に正解から遠ざかっている気さえします。
 その後もいろいろな代案を考えたのですが、なかなかうまくいかずに月日が経って行きました。
まあ納期があるわけでもないので、手持ち無沙汰な時間に頭の中でちょっと考えてみる、
といった程度の極めて断続的な楽しみ方をしていたのですが・・・。
そして最近、ボケ防止も兼ねて(笑)、ちょっと本腰を入れて考えてみる事にしたのです。
しかし今までのように思い付きで無作為に試してもそう簡単に解決できる程
生易しいパズルではないという事に気づきました。
何らかの戦略的な指針が必要なのです。
そこで、まず考えた事は以下の様な指針でした。
もし、3階建てへの拡張に留まらず、
n階建てのスイッチにも拡張できる可能性があるならば、
このパズルの解答は、必ずや「美しい対称性」を持っているはずだ。
それを実現するためには各階のスイッチは対等の構造を持つべきであり、
よって、各スイッチは複数の配線同士の接続関係を切替えるタイプになるだろう、
と考えました。
また、ONとOFFで対称構造を維持するためには、
各階のスイッチは2値や4値といった偶数値であるべきで、
もっともシンプルで美しい解として、まずは2値を採択すべきと考えました。
また、同様の理由から配線数も偶数でなければならいとも考えました。
2階建ての2本に対して、次の偶数は4本です。
そこで、3階建ての階段スイッチには最低でも4配線が必要だという仮説を立てました。
その後もいろいろな代案を考えたのですが、なかなかうまくいかずに月日が経って行きました。
まあ納期があるわけでもないので、手持ち無沙汰な時間に頭の中でちょっと考えてみる、
といった程度の極めて断続的な楽しみ方をしていたのですが・・・。
そして最近、ボケ防止も兼ねて(笑)、ちょっと本腰を入れて考えてみる事にしたのです。
しかし今までのように思い付きで無作為に試してもそう簡単に解決できる程
生易しいパズルではないという事に気づきました。
何らかの戦略的な指針が必要なのです。
そこで、まず考えた事は以下の様な指針でした。
もし、3階建てへの拡張に留まらず、
n階建てのスイッチにも拡張できる可能性があるならば、
このパズルの解答は、必ずや「美しい対称性」を持っているはずだ。
それを実現するためには各階のスイッチは対等の構造を持つべきであり、
よって、各スイッチは複数の配線同士の接続関係を切替えるタイプになるだろう、
と考えました。
また、ONとOFFで対称構造を維持するためには、
各階のスイッチは2値や4値といった偶数値であるべきで、
もっともシンプルで美しい解として、まずは2値を採択すべきと考えました。
また、同様の理由から配線数も偶数でなければならいとも考えました。
2階建ての2本に対して、次の偶数は4本です。
そこで、3階建ての階段スイッチには最低でも4配線が必要だという仮説を立てました。
 3階建ての4本配線において、2値のスイッチで対称性を維持するために、
各階のスイッチは、2配線を接続し他の2配線を断線する、という構造になっているはずです。
つまり、スイッチの切替えで2配線が入れ替わるという対称構造を仮定しました。
この条件下で、各階のスイッチが互いに補間し合う様なパターンを模索すれば良いのです。
この指針を元に試行錯誤した結果、ついに解を見つける事が出来ました!
以下がそのスイッチ構造です。
3階建ての4本配線において、2値のスイッチで対称性を維持するために、
各階のスイッチは、2配線を接続し他の2配線を断線する、という構造になっているはずです。
つまり、スイッチの切替えで2配線が入れ替わるという対称構造を仮定しました。
この条件下で、各階のスイッチが互いに補間し合う様なパターンを模索すれば良いのです。
この指針を元に試行錯誤した結果、ついに解を見つける事が出来ました!
以下がそのスイッチ構造です。
 このパターンでスイッチを組み合わせれば、他の階がどの様な状態になっていても
対象とする階の切替えで照明のON/OFFを制御できます。
しかもどの階のスイッチも2値ですから、
利用者からすれば2階建てのスイッチと同様の操作感や外観を持ちます。
各階を結ぶ配線が4本に増えますが、それほどのコストアップにならないでしょう。
実用性も充分にあると思えます。
しかし実用性うんぬんよりも、その美しい対称性に満足感を感じます。
対称性が満たされているため、各階のスイッチの構造も共通化できる事も思い付きました。
例えば、以下の図のようにT字型のレバーを用意してT字の中程に支点を設けます。
つまみを左に動かすと、右側の2つの端子を上下に接続し、左側の上下2つの端子を開放します。
このパターンでスイッチを組み合わせれば、他の階がどの様な状態になっていても
対象とする階の切替えで照明のON/OFFを制御できます。
しかもどの階のスイッチも2値ですから、
利用者からすれば2階建てのスイッチと同様の操作感や外観を持ちます。
各階を結ぶ配線が4本に増えますが、それほどのコストアップにならないでしょう。
実用性も充分にあると思えます。
しかし実用性うんぬんよりも、その美しい対称性に満足感を感じます。
対称性が満たされているため、各階のスイッチの構造も共通化できる事も思い付きました。
例えば、以下の図のようにT字型のレバーを用意してT字の中程に支点を設けます。
つまみを左に動かすと、右側の2つの端子を上下に接続し、左側の上下2つの端子を開放します。
 このようなスイッチがあれば、配線の接続の仕方だけで各階のパターンを実現できます。
例えば、
1階は左側端子にA線とB線を接続し、右側端子にC線とD線をつなぎます。
2階は左側端子にA線とC線を接続し、右側端子にB線とD線をつなぎます。
このようなスイッチがあれば、配線の接続の仕方だけで各階のパターンを実現できます。
例えば、
1階は左側端子にA線とB線を接続し、右側端子にC線とD線をつなぎます。
2階は左側端子にA線とC線を接続し、右側端子にB線とD線をつなぎます。
 むろん、3階の接続も同様な方法で実現できます。
一々、各階用のスイッチを製作する必要は無いのです。
美しい設計はハードウェアの無駄も取り除く、という典型的な例だと思います。
むろん、3階の接続も同様な方法で実現できます。
一々、各階用のスイッチを製作する必要は無いのです。
美しい設計はハードウェアの無駄も取り除く、という典型的な例だと思います。
 さてこれで当初設定した“パズル”は一応解けました。
しかし“パズル”を“思索”に昇華させるには、ここで終わらせてはいけません。
実はここから思索としては面白く美味しいプロセスなのです。
アルキメデスを例に挙げるのはおこがましいのですが、彼が風呂に体を沈めた時、
湯船から溢れるお湯を見て王冠の体積を測定する方法を思い付いた瞬間が
“パズル”を解いたポイントとすれば、更にそこから浮力の法則を導き出すプロセスこそが
“思索”の領域と言えるでしょう。
「王冠」の方は多分納期があったでしょうが、「浮力」の方は無かったはずです。
思索への取っ掛かりとして3階建ての階段スイッチの解を4階建てに拡張する事を試み、
その拡張過程で背後に存在するであろうより普遍的なものを感じ取って見ようと思いました。
その副次成果として、n階建てへの拡張方式も得られるはずです。
まず、3階建ての階段スイッチで用いた4配線を、正方形の頂点(A,B,C,D)として配置します。
そして、各階のスイッチパターンがどの様になるかを確認します。
幾何的なアプローチにより、背後に潜む美しい何かが見えてくるのではないかと思ったのです。
その効能は直ぐに現れました。
1階と2階は互いに向かい合う辺を、上下もしくは左右に切替えるパターンである事が判ります。
そして3階は、2つある対角線を切替えるパターンになっています。
なかなか美しい関係が見えてきました。
2つ頂点の組合せを切替える方法は、これ以外にありません。唯一無二のセットです。
さてこれで当初設定した“パズル”は一応解けました。
しかし“パズル”を“思索”に昇華させるには、ここで終わらせてはいけません。
実はここから思索としては面白く美味しいプロセスなのです。
アルキメデスを例に挙げるのはおこがましいのですが、彼が風呂に体を沈めた時、
湯船から溢れるお湯を見て王冠の体積を測定する方法を思い付いた瞬間が
“パズル”を解いたポイントとすれば、更にそこから浮力の法則を導き出すプロセスこそが
“思索”の領域と言えるでしょう。
「王冠」の方は多分納期があったでしょうが、「浮力」の方は無かったはずです。
思索への取っ掛かりとして3階建ての階段スイッチの解を4階建てに拡張する事を試み、
その拡張過程で背後に存在するであろうより普遍的なものを感じ取って見ようと思いました。
その副次成果として、n階建てへの拡張方式も得られるはずです。
まず、3階建ての階段スイッチで用いた4配線を、正方形の頂点(A,B,C,D)として配置します。
そして、各階のスイッチパターンがどの様になるかを確認します。
幾何的なアプローチにより、背後に潜む美しい何かが見えてくるのではないかと思ったのです。
その効能は直ぐに現れました。
1階と2階は互いに向かい合う辺を、上下もしくは左右に切替えるパターンである事が判ります。
そして3階は、2つある対角線を切替えるパターンになっています。
なかなか美しい関係が見えてきました。
2つ頂点の組合せを切替える方法は、これ以外にありません。唯一無二のセットです。
 では4階建ての場合は、この美しい対称性をどの様に拡張すれば良いのでしょうか?
論理的アプローチではなく、美的アプローチで試してみました。
すなわち3階建てと同様の対称性が保たれるはずであるという仮説です。
指針では、配線数は偶数であると仮定していました。
そして、3階建てでの4本配線は唯一無二に充足しているため、
4階建てはそれよりも多い配線が必要なはずです。つまり、次の偶数6本となります。
そこで3階建ての時と同様に、六角形の頂点を配線経路と見なして
いろいろと試行錯誤をしたのですが、6本ではなかなかうまくいきませんでした。
そこで、次の配線数を試みる事にしました。つまり8本です。
そして8本ともなると、八角形よりももっと魅力的な
幾何イメージの飛躍が可能である事に気づきました。
3階建ての「正方形」に対し、4階建ては「立方体」を構築できるのです。
つまり、2次元から3次元に拡張される訳です。
そして、スイッチの切替えパターンの組み合わせは、
3階建てが「辺」だった事から、4階建ては「面」になるだろうと予測できます。
では4階建ての場合は、この美しい対称性をどの様に拡張すれば良いのでしょうか?
論理的アプローチではなく、美的アプローチで試してみました。
すなわち3階建てと同様の対称性が保たれるはずであるという仮説です。
指針では、配線数は偶数であると仮定していました。
そして、3階建てでの4本配線は唯一無二に充足しているため、
4階建てはそれよりも多い配線が必要なはずです。つまり、次の偶数6本となります。
そこで3階建ての時と同様に、六角形の頂点を配線経路と見なして
いろいろと試行錯誤をしたのですが、6本ではなかなかうまくいきませんでした。
そこで、次の配線数を試みる事にしました。つまり8本です。
そして8本ともなると、八角形よりももっと魅力的な
幾何イメージの飛躍が可能である事に気づきました。
3階建ての「正方形」に対し、4階建ては「立方体」を構築できるのです。
つまり、2次元から3次元に拡張される訳です。
そして、スイッチの切替えパターンの組み合わせは、
3階建てが「辺」だった事から、4階建ては「面」になるだろうと予測できます。
 さて、問題は4階部分の切替えスイッチのパターンです。3階建てでは「対角線」でした。
しかし立方体の対角線は4本あるため、対称性が崩れます。
対称性を実現するためには共役関係が成り立っている必要があると直感しました。
しかも、4階建てのパターンは4つの頂点から構築される必要がありますが、
単純な対角線ではその端点である2つの頂点しか含まれません。
2値の切替えつまり共役性を満たし、4頂点を含む描像は如何なるものになるでしょうか?
見つけました!
それが、下記の図になります。
さて、問題は4階部分の切替えスイッチのパターンです。3階建てでは「対角線」でした。
しかし立方体の対角線は4本あるため、対称性が崩れます。
対称性を実現するためには共役関係が成り立っている必要があると直感しました。
しかも、4階建てのパターンは4つの頂点から構築される必要がありますが、
単純な対角線ではその端点である2つの頂点しか含まれません。
2値の切替えつまり共役性を満たし、4頂点を含む描像は如何なるものになるでしょうか?
見つけました!
それが、下記の図になります。
 これは立方体の内側に存在する立体で、よく見ると正四面体となっています。
しかも立方体の中にはこの2つしか存在せず、共役性を満たしながら解が一意に決まります。
私はこれを、立方体の「対角面」と名付けたいと思います。
まさに、正方形の「対角線」の拡張です。
今回の思索テーマは階段スイッチの拡張であった訳ですが、
図らずも対角線の次元を1つ上げた描像を得た事になります。
なんと美しい形状でしょうか!
★ 正直、この双対な「対角面」の発見が、今回の思索の中で最も興奮した瞬間でした!
さて、階段スイッチのテーマに戻しましょう。
以上で得た4階建ての階段スイッチを、そのパターンとして描くと以下のようになります。
これは立方体の内側に存在する立体で、よく見ると正四面体となっています。
しかも立方体の中にはこの2つしか存在せず、共役性を満たしながら解が一意に決まります。
私はこれを、立方体の「対角面」と名付けたいと思います。
まさに、正方形の「対角線」の拡張です。
今回の思索テーマは階段スイッチの拡張であった訳ですが、
図らずも対角線の次元を1つ上げた描像を得た事になります。
なんと美しい形状でしょうか!
★ 正直、この双対な「対角面」の発見が、今回の思索の中で最も興奮した瞬間でした!
さて、階段スイッチのテーマに戻しましょう。
以上で得た4階建ての階段スイッチを、そのパターンとして描くと以下のようになります。
 大変複雑そうでボリューム感のある結果となりました。
しかしここでも各階スイッチは2値であり、しかも前述のT字スイッチがそのまま利用できます!
各端子に接続される配線が2本から4本に増えるだけです。
実際にこのパターンが目的を達成しているかどうかを確認するために、
簡単なプログラムを作って、あらゆる状態からON/OFF操作が出来る事も確認しました。
計算機は問題を解くことは苦手ですが、成否を検証するのは得意ですね(笑)。
大変複雑そうでボリューム感のある結果となりました。
しかしここでも各階スイッチは2値であり、しかも前述のT字スイッチがそのまま利用できます!
各端子に接続される配線が2本から4本に増えるだけです。
実際にこのパターンが目的を達成しているかどうかを確認するために、
簡単なプログラムを作って、あらゆる状態からON/OFF操作が出来る事も確認しました。
計算機は問題を解くことは苦手ですが、成否を検証するのは得意ですね(笑)。
 さて、2階建ての階段スイッチを3階建て、4階建てへと進めてきました。
その手法は対称性をベースにした類推と、幾何的な考察が中心でした。
幾何的な考察は直感的であり状態の把握も容易なのですが、いかんせん拡張は3次元空間までです。
n階建てに駒を進めるには、論理学か代数的なアプローチに方針を変更するしかありません。
そこで4階建ての階段スイッチの解を以下のように書き表し、その規則性を考察してみる事にします。
さて、2階建ての階段スイッチを3階建て、4階建てへと進めてきました。
その手法は対称性をベースにした類推と、幾何的な考察が中心でした。
幾何的な考察は直感的であり状態の把握も容易なのですが、いかんせん拡張は3次元空間までです。
n階建てに駒を進めるには、論理学か代数的なアプローチに方針を変更するしかありません。
そこで4階建ての階段スイッチの解を以下のように書き表し、その規則性を考察してみる事にします。
 一種のマトリックスです。
左から右に各配線経路(A,B,C,・・・)を並べ、下から上に各階を積上げます。
すなわち、各列は全階を貫く配線を表し、各行はその階のスイッチを表します。
各欄にはスイッチの状態として、1で導通を、0で断線を表わす様に数値を与えておきます。
2階のスイッチを切替える操作は、2階の行の1と0を全て反転させる事に相当します。
一種のマトリックスです。
左から右に各配線経路(A,B,C,・・・)を並べ、下から上に各階を積上げます。
すなわち、各列は全階を貫く配線を表し、各行はその階のスイッチを表します。
各欄にはスイッチの状態として、1で導通を、0で断線を表わす様に数値を与えておきます。
2階のスイッチを切替える操作は、2階の行の1と0を全て反転させる事に相当します。
 階段スイッチのパズルとは、結局このマトリックスを導き出す事にあります。
既に得られてる3階建てのマトリックスから、4階建てのマトリックスを導く方法を考えてみましょう。
(1)まず3階建てマトリックス(これは4×4行列)を点灯状態にしておきます。
→これを点灯ブロックと呼びます。
(2)そして消灯状態マトリックス(これも4×4行列)も用意します。
→これを消灯ブロックと呼びます。
※点灯(1)から消灯(2)へと状態を変えるには、
どこか1つの階のスイッチを反転(切替え)すればすぐに得る事が出来ます。
(3)この点灯ブロックと消灯ブロックを横に並べ、1階部分に新しいスイッチ(行)を挿入します。
その新しい行の各列の値はとても単純なルールで与えます。
そのルールとは、「点灯ブロック直下は1、消灯ブロックの直下は0」です。
これで4階建てのマトリックスが出来上がります。
階段スイッチのパズルとは、結局このマトリックスを導き出す事にあります。
既に得られてる3階建てのマトリックスから、4階建てのマトリックスを導く方法を考えてみましょう。
(1)まず3階建てマトリックス(これは4×4行列)を点灯状態にしておきます。
→これを点灯ブロックと呼びます。
(2)そして消灯状態マトリックス(これも4×4行列)も用意します。
→これを消灯ブロックと呼びます。
※点灯(1)から消灯(2)へと状態を変えるには、
どこか1つの階のスイッチを反転(切替え)すればすぐに得る事が出来ます。
(3)この点灯ブロックと消灯ブロックを横に並べ、1階部分に新しいスイッチ(行)を挿入します。
その新しい行の各列の値はとても単純なルールで与えます。
そのルールとは、「点灯ブロック直下は1、消灯ブロックの直下は0」です。
これで4階建てのマトリックスが出来上がります。
 以上は3階建てから4階建てを導く手順ですが、
この手続きは「n階建て」から「n+1階建て」を導く一般的な方法として成り立ちます。
実は、新しく挿入する行は1階である必要は無く、どの階の位置でも問題はありませんし、
その挿入した行の値は「点灯ブロック直下が0で、消灯ブロック直下が1」でも構いません。
(照明の初期状態が、点灯なのか消灯なのかが変わるだけです)
この手続きの論理的な背景は、以下に寄ります。
以上は3階建てから4階建てを導く手順ですが、
この手続きは「n階建て」から「n+1階建て」を導く一般的な方法として成り立ちます。
実は、新しく挿入する行は1階である必要は無く、どの階の位置でも問題はありませんし、
その挿入した行の値は「点灯ブロック直下が0で、消灯ブロック直下が1」でも構いません。
(照明の初期状態が、点灯なのか消灯なのかが変わるだけです)
この手続きの論理的な背景は、以下に寄ります。
 どうやら正しく機能しているようです。
以上の手続きの論理的帰結として、
n階建ての階段スイッチには、2の(n-1)乗の配線が必要
という規則が導けます。
どうやら正しく機能しているようです。
以上の手続きの論理的帰結として、
n階建ての階段スイッチには、2の(n-1)乗の配線が必要
という規則が導けます。
 比較的簡単な手順で何階建てでも解を得られる事が判ったので、
6階建てのマトリックスを描いてみました。
配線は32本にもなりますが、ルールは単純なので簡単です。
そして、このマトリックスを描く過程で、
各階に割り当てるスイッチ配列を整理していたら、更に見通しが良くなる事に気づきました。
比較的簡単な手順で何階建てでも解を得られる事が判ったので、
6階建てのマトリックスを描いてみました。
配線は32本にもなりますが、ルールは単純なので簡単です。
そして、このマトリックスを描く過程で、
各階に割り当てるスイッチ配列を整理していたら、更に見通しが良くなる事に気づきました。
 1階は、1と0が交互に並ぶパターン。
2階は、1が2回、0が2回と繰り返すパターン。
3階は、1が4回、0が4回と繰り返すパターン。
・・・
といった感じです。
結局、nを対象とする階数とすると、
各階のスイッチパターンは、2の(n-1)乗の周期で1と0を繰り返せば良い事になります。
しかるに、最上階だけは周期が乱れます。
最上階は、点灯ブロックと消灯ブロックの分離を一身に背負っており、
反転してコピーする過程を繰り返すために、結果として周期を見出せないパターンになるのです。
1階は、1と0が交互に並ぶパターン。
2階は、1が2回、0が2回と繰り返すパターン。
3階は、1が4回、0が4回と繰り返すパターン。
・・・
といった感じです。
結局、nを対象とする階数とすると、
各階のスイッチパターンは、2の(n-1)乗の周期で1と0を繰り返せば良い事になります。
しかるに、最上階だけは周期が乱れます。
最上階は、点灯ブロックと消灯ブロックの分離を一身に背負っており、
反転してコピーする過程を繰り返すために、結果として周期を見出せないパターンになるのです。
 しかし、この最上階の1と0の並びを注意深く観察してみると、
反転コピー方式で解を得る以外に、もう一つ別のやり方がある事に気づきました。
この新しい方式の方が、計算をアルゴリズム化したり、数式化するに有利かもしれません。
まず、1は「1と0」に、0は「0と1」に“増殖”するという基本ルールを設定します。
しかし、この最上階の1と0の並びを注意深く観察してみると、
反転コピー方式で解を得る以外に、もう一つ別のやり方がある事に気づきました。
この新しい方式の方が、計算をアルゴリズム化したり、数式化するに有利かもしれません。
まず、1は「1と0」に、0は「0と1」に“増殖”するという基本ルールを設定します。
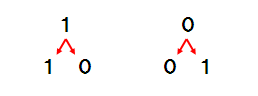 そして、ただ一つの1を“種”として階層的な増殖プロセスを開始します。
その様子を示したのが次の図です。
そして、ただ一つの1を“種”として階層的な増殖プロセスを開始します。
その様子を示したのが次の図です。
 いかがでしょうか。
図の最後の階層には6階建てにおける最上階スイッチパターンが現れているのが判ると思います。
実はこの階層図は、各階層がそれぞれの階数の最上階スイッチパターンに符合しているのです。
この階層図は、よくよく眺めていると面白い性質を持っている事が判ります。
どのノードから始めても、左側に降りて行く階層は全体と部分が一致しています。
逆に、右側に降りて行く階層は全体と部分が正反対の値を持っているのです。
まるで、フラクタルと反フラクタルがハイブリッドになっているような構造ですね。
いかがでしょうか。
図の最後の階層には6階建てにおける最上階スイッチパターンが現れているのが判ると思います。
実はこの階層図は、各階層がそれぞれの階数の最上階スイッチパターンに符合しているのです。
この階層図は、よくよく眺めていると面白い性質を持っている事が判ります。
どのノードから始めても、左側に降りて行く階層は全体と部分が一致しています。
逆に、右側に降りて行く階層は全体と部分が正反対の値を持っているのです。
まるで、フラクタルと反フラクタルがハイブリッドになっているような構造ですね。
 2階建ての階段のスイッチが、
実にシンプルな回路で鮮やかな制御をしているという驚きに端を発して、
最後は、このように面白く不思議な階層図に達する事が出来ました。
この階層構造がどんな意味を持っているか、今のところ私にも判りません。
ただ、愉快なイメージは膨らむのです。
今、この宇宙空間全体が無数のスイッチで埋められていて、
それらは隣り合うスイッチにだけ接続されているとします。まあ、一種の近接作用ですね。
にも関わらず、どのスイッチを局所的に切替えても全体に影響を与える制御ができるのです。
その制御を可能にする条件は、
「極めて周期性の高いパターンと、不思議な階層を持つパターンで構成される」
という事を示唆しているのかもしれません。
何か深遠なものを感じさせる今回の思索の旅でした。
2階建ての階段のスイッチが、
実にシンプルな回路で鮮やかな制御をしているという驚きに端を発して、
最後は、このように面白く不思議な階層図に達する事が出来ました。
この階層構造がどんな意味を持っているか、今のところ私にも判りません。
ただ、愉快なイメージは膨らむのです。
今、この宇宙空間全体が無数のスイッチで埋められていて、
それらは隣り合うスイッチにだけ接続されているとします。まあ、一種の近接作用ですね。
にも関わらず、どのスイッチを局所的に切替えても全体に影響を与える制御ができるのです。
その制御を可能にする条件は、
「極めて周期性の高いパターンと、不思議な階層を持つパターンで構成される」
という事を示唆しているのかもしれません。
何か深遠なものを感じさせる今回の思索の旅でした。
 (2011.09.17追記)
上記の様な考察を綿々と綴ってきましたが、昨日匿名の方から以下のメールを頂きました。
やはりこの命題は既知のものであり、しかももっとエレガントな解法が存在していました。
情報のご提供ありがとうございました。
●3路・4路スイッチ
なんと、どの様な階数であろうとも2本の配線で階段のスイッチを実現しています。
実に鮮やかです!
2階の階段スイッチは「3路スイッチ」と呼ばれ、
更にどの階数でも可能とするためのスイッチは「4路スイッチ」と呼ばれているそうです。
しっかりと名称が与えられているということは、既に業界では常識化されているという事ですね。
特筆すべきは、上記の解法は3路スイッチと4路スイッチの組合せになっているという事です。
1階と最上階は3路スイッチを、間の階は4路スイッチを使用しています。
私が解を得ようとする過程で「対称性」という方針を打ち立てた時点で、
この4路スイッチとは別の方向に進んでしまったようです。
私の到達した方式でも問題は解決するのですが、階が増すごとに配線が指数的に増え実用的ではない。
それに比べて4路スイッチのエレガントさは、見事としか言い様がありません。
私はひどく遠回りしていたどころか、最終的な“階”いや“解”に到達できなかったみたいです。orz
でも逆に“サイト検索”に頼らず最後まで自分の力で考え抜こう、という姿勢で
私が思索に臨んでいる事は示せたかもしれませんね・・・(苦笑)
(2011.09.17追記)
上記の様な考察を綿々と綴ってきましたが、昨日匿名の方から以下のメールを頂きました。
やはりこの命題は既知のものであり、しかももっとエレガントな解法が存在していました。
情報のご提供ありがとうございました。
●3路・4路スイッチ
なんと、どの様な階数であろうとも2本の配線で階段のスイッチを実現しています。
実に鮮やかです!
2階の階段スイッチは「3路スイッチ」と呼ばれ、
更にどの階数でも可能とするためのスイッチは「4路スイッチ」と呼ばれているそうです。
しっかりと名称が与えられているということは、既に業界では常識化されているという事ですね。
特筆すべきは、上記の解法は3路スイッチと4路スイッチの組合せになっているという事です。
1階と最上階は3路スイッチを、間の階は4路スイッチを使用しています。
私が解を得ようとする過程で「対称性」という方針を打ち立てた時点で、
この4路スイッチとは別の方向に進んでしまったようです。
私の到達した方式でも問題は解決するのですが、階が増すごとに配線が指数的に増え実用的ではない。
それに比べて4路スイッチのエレガントさは、見事としか言い様がありません。
私はひどく遠回りしていたどころか、最終的な“階”いや“解”に到達できなかったみたいです。orz
でも逆に“サイト検索”に頼らず最後まで自分の力で考え抜こう、という姿勢で
私が思索に臨んでいる事は示せたかもしれませんね・・・(苦笑)