表紙に戻る
色の立方体
「色」は思索テーマとして魅力的なものらしく、実に多岐に渡る分野の著名人たちがいろいろ
な角度から考察を加えてきました。ギリシア時代には、タレス・プラトン・アリストレテス・
ピタゴラスなどが哲学的な観点から考察し、中世には錬金術と関わりながら諸説が生み出されました。
画家としてのレオナルド・ダ・ビンチは、色彩調和の立場から色彩遠近法をまとめ上げました。
物理学者ニュートンは、それまで色が物質の属性と考えられていたのに対し、色自体が独立した
存在である事を主張し、色の粒子説を唱えました。対してホイヘンスは色の波動説を提唱し、
その後、ヤングやフレネルらの実験により光の波動的性質が解明されていきました。
一方、文豪のゲーテは「光と闇の境界線にこそ色は存在する」とし“色彩論”を書きました。
“最も重要な著作は、戯曲ファウストではなく色彩論である”とゲーテ自身は語っています。
「色彩は、なかば光、なかば影である。そして、光と闇の結婚である」
物理的なニュートンの色の捉え方に真っ向から対峙したゲーテ。
その長大な“色彩論”を刊行したのは60歳の時です。
現在、可視光線は電磁波のある周波数帯であることが知られており、色はその周波数の違いに
対応していることが解明されています。下図が、それを表す光のスペクトルです。
「スペクトル」という言葉は、ニュートンが命名しました。
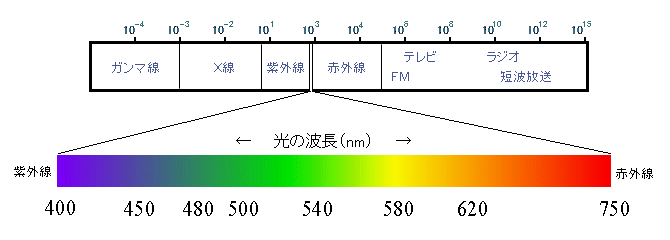 ちなみにニュートンは、このスペクトルが7色よりなると主張しましたが、それは彼が音楽理論
との関係を意識したのだと言われています。彼は音程と色とを結びつけたかったのかもしれません。
ニュートンは、ピタゴラスやプラトンのように「神の調和」を強く意識する人物だったようです。
1936年にサザビーズのオークションにかけられたニュートンの秘密メモの中には、意外にも「錬金術」
に関するくだりがびっしり書かれているものがあったそうです。近代科学の扉を開けた天才ニュートン
も、まだ神秘的な時代の空気の中で生きていたのだ、ということを思い知らされる話です。
さて、20世紀に入ると色彩を体系的に把握する研究が起りました。
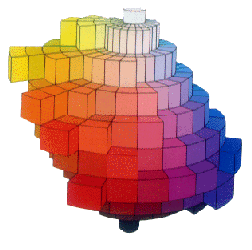
画家のマンセルが考案した色立体モデル(1905年)は、現代でもインテリアなどに利用され
ているシステムです。明度を上下に取り、白を頂点に黒を底点に配置します。その軸を
中心に色相で取囲み、彩度が上がるにつれて周辺に広げていきます。
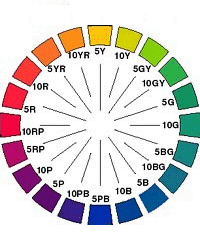
心理的な色相をベースに構築されているため、全体の構造がデコボコしています。(左図)
真上から見ると、色相環と呼ばれる心理色相のリングが見られます。(右図)
これは、物理学的には1次元に並べられる周波数の対応色を、心理学的に輪状に組立て
直したと言えます。ちょっぴりゲーテの主張が感じられます。
ちなみにニュートンは、このスペクトルが7色よりなると主張しましたが、それは彼が音楽理論
との関係を意識したのだと言われています。彼は音程と色とを結びつけたかったのかもしれません。
ニュートンは、ピタゴラスやプラトンのように「神の調和」を強く意識する人物だったようです。
1936年にサザビーズのオークションにかけられたニュートンの秘密メモの中には、意外にも「錬金術」
に関するくだりがびっしり書かれているものがあったそうです。近代科学の扉を開けた天才ニュートン
も、まだ神秘的な時代の空気の中で生きていたのだ、ということを思い知らされる話です。
さて、20世紀に入ると色彩を体系的に把握する研究が起りました。
画家のマンセルが考案した色立体モデル(1905年)は、現代でもインテリアなどに利用され
ているシステムです。明度を上下に取り、白を頂点に黒を底点に配置します。その軸を
中心に色相で取囲み、彩度が上がるにつれて周辺に広げていきます。
心理的な色相をベースに構築されているため、全体の構造がデコボコしています。(左図)
真上から見ると、色相環と呼ばれる心理色相のリングが見られます。(右図)
これは、物理学的には1次元に並べられる周波数の対応色を、心理学的に輪状に組立て
直したと言えます。ちょっぴりゲーテの主張が感じられます。
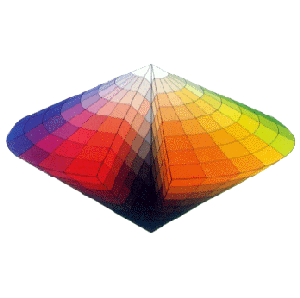
ノーベル化学賞受賞者であり、アマチュア画家でもあったオストワルドは、理想的な白色・黒色・純色
の混合量によってすべての色を表すという考えに基づき、新しい色立体モデル(1918年)を考案しました。
「調和は秩序に等しい」という定義に基づいて、この立体モデルで配色調和論を提唱した“色彩論”は、
彼が65歳の時の論文です。文豪と化学者という違いはありますが、まるでゲーテのようです。実際、
白色量、黒色量に色相を加えた3つの混合で色を表現するモデルですから、ゲーテの“光と影の結婚”
に似ているとも言えます。従って、マンセルのモデルにある、明度、彩度という考え方はありません。
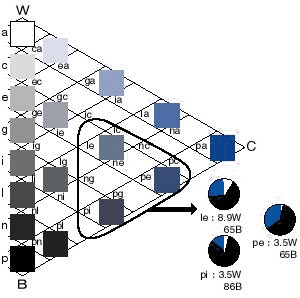
オストワルドのモデルは、混合率という数値的規則で組立てられ、綺麗な円盤形状になります。(左図)
同色相断面は正三角形になり、三角形内部の各区画は色の混合率を示すアルファベット記号によって
位置が表されます。(右図)
現在では、これらの色モデルの他にも、いろいろな特徴を持つ多くのモデルが立案されています。
「PCCS(日本色研配色体系)」「CMYK(インク表示系)」「CIE(XYZ系色度座標)」
「CIE(L*u*v*色空間)」「CIE(L*C*H*色空間)」「CIE(L*a*b*色空間)」などなど、
私にはとてもすべてを把握できません。“日本色彩学会”や“(社団法人)日本流行色協会”なるもの
も存在しています。また、商工会議所が主催する“カラーコーディネーター検定”や、文部科学省認定
の“色彩検定(AFT)”もあります。これらを受験する方は、この辺の知識と概念をしっかり把握しなけ
ればならないんでしょうね。
さて、心理的な色の体系化が進む一方、生物学・生理学的とも言えるアプローチも存在しました。
1801年、ヤングは絵の具の混色からヒントを得て、視神経には赤・緑・青の三色を感じる神経があり、
すべての色はこの三つの神経の刺激の割合で知覚されるという仮説を立てました。
1868年、ヘルムホルツはこのヤングの仮説を視細胞と関連付けて説明することに成功します。
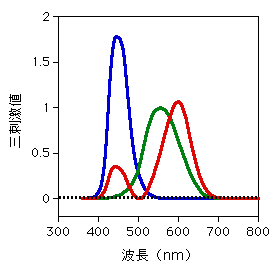 人間には、ある特定の波長の光に反応する細胞が3種類あり、
それがちょうど赤・緑・青の3つの色で表現される光で鋭い
感度ピークを示します。
この3つの波長(赤緑青)以外の光が視神経にあたると、複数
の細胞が適当な比率で刺激されるため、その案配で私たちは
色を識別しているわけです。
神の存在を信じたくなるような凄いシステムです。
それにしても、何故“3”なのでしょう? 内耳に存在する
三半規管は、空間が3次元であるという根拠があるにしても、
そもそも空間自体が“3”つの方向を持っている。
遺伝子情報の最小単位トリプレットも“3”です。
素粒子バリオンにおける構成クォークも3つ。
神様は、よほど“3”という数字がお好きなようです。(笑)
人間には、ある特定の波長の光に反応する細胞が3種類あり、
それがちょうど赤・緑・青の3つの色で表現される光で鋭い
感度ピークを示します。
この3つの波長(赤緑青)以外の光が視神経にあたると、複数
の細胞が適当な比率で刺激されるため、その案配で私たちは
色を識別しているわけです。
神の存在を信じたくなるような凄いシステムです。
それにしても、何故“3”なのでしょう? 内耳に存在する
三半規管は、空間が3次元であるという根拠があるにしても、
そもそも空間自体が“3”つの方向を持っている。
遺伝子情報の最小単位トリプレットも“3”です。
素粒子バリオンにおける構成クォークも3つ。
神様は、よほど“3”という数字がお好きなようです。(笑)
こうして、人間にとっての光の三原色は、赤・緑・青(RGB)であることが解明されました。
考えてみると、これは人間にとっての話であり、他の動物では異なっていることでしょう。
また、同じ人間でもRGBの各感度に個人差があるのかもしれません。
 さて、ここまでは先人達が築き上げた既知の発見や発案です。
私は一介の凡人にすぎませんが、恐れながら、私も少々色についての“思索”を行いましたので、
ここでご披露することにします。もちろん、すでに当然のように発見されていることで、私がそれ
を知らないだけかもしれませんが、私自身の“思索”でたどり着いたお話であることは神に誓います。
・・・と、大袈裟な前置をしましたが、大した発見ではありません。(笑)
マンセルの色立体モデルを中学の美術の教科書で知った私は、その何やら歪(いびつ)な形状に
一種の不満を感じました。色の体系は何故このようにデコボコしているんだろう? 本当は、
もっと美しいモデルが存在しているのではないだろうか?(その当時私はオストワルドのモデル
を知りませんでした)そのような気持を胸に抱きつつ月日が経ち、私はコンピューターに接する
ようになりました。そこで、光の三原色というものをグラフィック・プログラミングという世界
を通じて体験することになります。ご存知のようにコンピューターの世界での色表現は、RGB
の組合せで行います。私は、このRGBの規格性をもっと前面に押出したモデルが作れるのでは
ないかと考えたのです。
さて、ここまでは先人達が築き上げた既知の発見や発案です。
私は一介の凡人にすぎませんが、恐れながら、私も少々色についての“思索”を行いましたので、
ここでご披露することにします。もちろん、すでに当然のように発見されていることで、私がそれ
を知らないだけかもしれませんが、私自身の“思索”でたどり着いたお話であることは神に誓います。
・・・と、大袈裟な前置をしましたが、大した発見ではありません。(笑)
マンセルの色立体モデルを中学の美術の教科書で知った私は、その何やら歪(いびつ)な形状に
一種の不満を感じました。色の体系は何故このようにデコボコしているんだろう? 本当は、
もっと美しいモデルが存在しているのではないだろうか?(その当時私はオストワルドのモデル
を知りませんでした)そのような気持を胸に抱きつつ月日が経ち、私はコンピューターに接する
ようになりました。そこで、光の三原色というものをグラフィック・プログラミングという世界
を通じて体験することになります。ご存知のようにコンピューターの世界での色表現は、RGB
の組合せで行います。私は、このRGBの規格性をもっと前面に押出したモデルが作れるのでは
ないかと考えたのです。
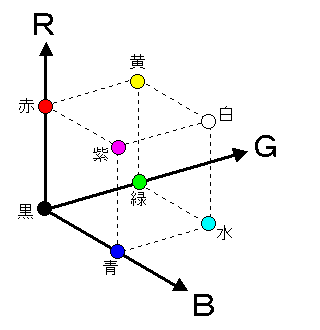 コンピュータの色指定はRGBの各輝度を指定し、
それを組合わせることで実現します。従って、
左図のようにR・G・Bの各輝度を各軸とした
3次元空間を設定すれば、すべての色がその座標
上にプロットされる事になります。しかも、輝度
は最大値を持っていますから空間内を無限に広が
るわけでなく、プロットされる領域は限定され、
それは立方体を形成します。
驚くべき事に、この立方体の中に世の中のすべて
の色が凝縮されていることになります。
コンピュータの色指定はRGBの各輝度を指定し、
それを組合わせることで実現します。従って、
左図のようにR・G・Bの各輝度を各軸とした
3次元空間を設定すれば、すべての色がその座標
上にプロットされる事になります。しかも、輝度
は最大値を持っていますから空間内を無限に広が
るわけでなく、プロットされる領域は限定され、
それは立方体を形成します。
驚くべき事に、この立方体の中に世の中のすべて
の色が凝縮されていることになります。
この「色の立方体」を、頂点が白、底点が黒になるように配置してみます。
このようにすると、色の位置関係がマンセルやオストワルドのモデルと似た状態になります。
上下方向に明度が与えられ、その無彩色の中心軸から離れるに従って彩度が高まります。
そして、中心軸を取囲むようにして色相の変化が見られます。
マンセルやオストワルドのモデルと異なるのは、色相環と呼ばれる同一平面上のリングが存在し
ないことです。むしろ、明度や彩度に反映される色成分の輝度が、配置の重要なファクターとなり、
RGBの輝度混合率の結果で色相が決るという性格を持っています。
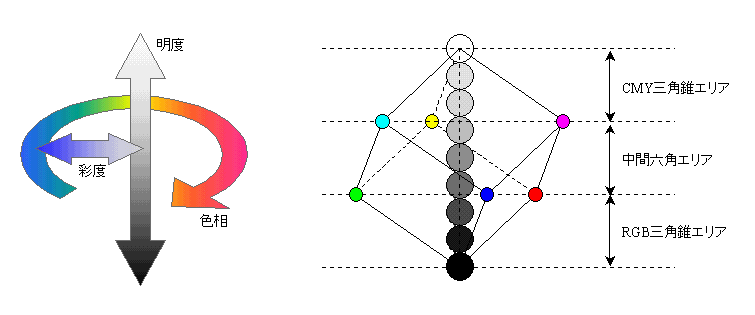 無彩色の中心軸と垂直に交わる平面で徐々にこの「色の立方体」を切っていくと、
3つの領域に分類されることがわかります。1つは白を頂点とした三角錐のエリアで、
この断面は正三角形を形成します。逆に黒を頂点とした三角錐のエリアが底側に存在します。
そしてその間には、断面が六角形となるエリアが存在しています。
以上が私の考えた「色の立方体」モデルです。
結果としては、あまりにも単純で誰にでも考え付きそうなものかもしれませんね。(笑)
しかし、ホームページやプログラミングでRGB指定に慣れ親しんでいても、これを
立体モデルとして把握するのは、ちょっとした思考の飛躍が必要だと思います。
事実、私もこのモデルを思い付いたのはRGBの制御を知って後、かなり経ってから
のことでした。このモデルを思い付いた時は、そのシンプルさが逆に嬉しかったのを
覚えています。
無彩色の中心軸と垂直に交わる平面で徐々にこの「色の立方体」を切っていくと、
3つの領域に分類されることがわかります。1つは白を頂点とした三角錐のエリアで、
この断面は正三角形を形成します。逆に黒を頂点とした三角錐のエリアが底側に存在します。
そしてその間には、断面が六角形となるエリアが存在しています。
以上が私の考えた「色の立方体」モデルです。
結果としては、あまりにも単純で誰にでも考え付きそうなものかもしれませんね。(笑)
しかし、ホームページやプログラミングでRGB指定に慣れ親しんでいても、これを
立体モデルとして把握するのは、ちょっとした思考の飛躍が必要だと思います。
事実、私もこのモデルを思い付いたのはRGBの制御を知って後、かなり経ってから
のことでした。このモデルを思い付いた時は、そのシンプルさが逆に嬉しかったのを
覚えています。

この「色の立方体」モデルが実際にはどのような色配置になるのか、
その内部の色配置にはどのようなグラデーションが見られるのか、
それらを実際に確認するフリーソフトを作ってみたので、ここに
公開いたします。
ソフトの名前は ColCube(カラーキューブ)と申します。
 ColCube(カラーキューブ)をダウンロードします
ColCube(カラーキューブ)をダウンロードします

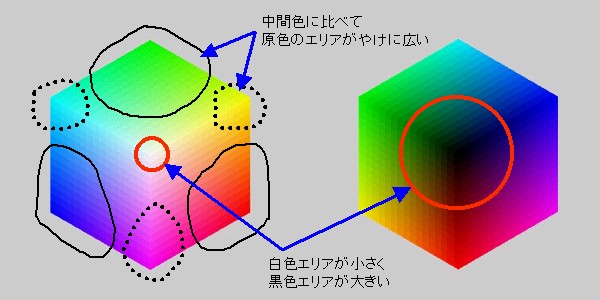
さて、この ColCube で「色の立方体」をいろいろな角度から観察していたら、
あることに気づきました。それは、
(1)中間色(水色・紫色・黄色)に比べ、三原色(RGB)のエリアがやけに広い
(2)白色のエリアに比べ、黒色のエリアがやけに広い
という2点です。
 そして、この2つの現象は以下の理由から生じるのではないかという1つの仮説を
立ててみました。両方とも同じ原因で起る現象と考えたのです。
そして、この2つの現象は以下の理由から生じるのではないかという1つの仮説を
立ててみました。両方とも同じ原因で起る現象と考えたのです。
|
人間は、明るい色の変化は敏感に感じるが、暗い色の変化は察知しにくい。
|
この仮説を“輝度と感度”の関係でグラフ化してみると以下のようになります。
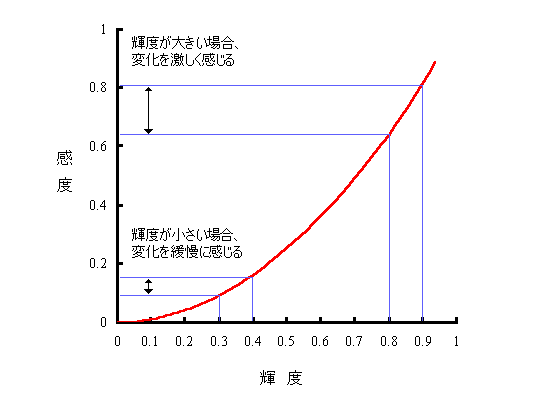 実際の曲線は、2次曲線なのか、3次曲線なのか、はたまたn次曲線なのか、
小数による次数の曲線なのか、それとも指数曲線なのか、あるいは非線形曲線なのか、
それは実際の測定でないと決定できませんが、とりあえず最もシンプルな2次曲線で
補正してみました。結果は以下のとおりです。
実際の曲線は、2次曲線なのか、3次曲線なのか、はたまたn次曲線なのか、
小数による次数の曲線なのか、それとも指数曲線なのか、あるいは非線形曲線なのか、
それは実際の測定でないと決定できませんが、とりあえず最もシンプルな2次曲線で
補正してみました。結果は以下のとおりです。
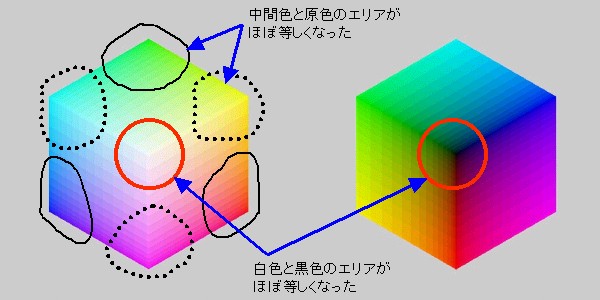 この結果を眺めると、なかなか良い具合に補正できているようです。
実際には、R・G・Bの各輝度の補正曲線の特性は、それぞれの視覚細胞によって
微妙に異なることでしょう。もし測定実験によりそれらの補正曲線が明確になれば、
「色の立方体」モデルは、その結果を容易に組込むことが出来ます。人間の持つ視覚
細胞と対応した生物学的補正が一意に行えるモデルなのです。
「色の立方体」モデル。それはとても単純で、しかもRGB値を並べただけという
極めて機械的なものです。しかし輝度補正を加えることで、物理的解釈と生理的解釈
がバランスした面白いモデルになったと思っています。
この結果を眺めると、なかなか良い具合に補正できているようです。
実際には、R・G・Bの各輝度の補正曲線の特性は、それぞれの視覚細胞によって
微妙に異なることでしょう。もし測定実験によりそれらの補正曲線が明確になれば、
「色の立方体」モデルは、その結果を容易に組込むことが出来ます。人間の持つ視覚
細胞と対応した生物学的補正が一意に行えるモデルなのです。
「色の立方体」モデル。それはとても単純で、しかもRGB値を並べただけという
極めて機械的なものです。しかし輝度補正を加えることで、物理的解釈と生理的解釈
がバランスした面白いモデルになったと思っています。
 (2015.11.03追記)
色の立体モデルと、それを視覚的に確認するソフトウェア(ColCube)を開発してから10年以上が経ちました。
このColCubeは、すべての色が立方体に綺麗に納まる様子を見ることに主眼を置いて開発しました。
そのため、一通りの確認を終えると、その後はあまり起動しないソフトになってしまいました。
色選択の機能も備えてはいますが、立体構造を立体のまま断面化するため、正直使いにくいのです。
そんな経緯で、「色選択」に主眼を置いたソフトウェアはどうあるべきか、が次の思索テーマとなりました。
市販のレイアウトツールや、色の指定を必要とするソフトには、必ず「色を選択」のパレットが備わっています。
共通して言えるのは、立体構造の色配列を何らかの工夫で平面化しているということです。
コンピューターのスクリーンは平面ですから、立体をそのまま扱うと操作がしにくくなるためでしょう。
例えば、Windows標準の色選択ダイアログは以下の様なものです。
[標準]タブ [ユーザー設定]タブ
(2015.11.03追記)
色の立体モデルと、それを視覚的に確認するソフトウェア(ColCube)を開発してから10年以上が経ちました。
このColCubeは、すべての色が立方体に綺麗に納まる様子を見ることに主眼を置いて開発しました。
そのため、一通りの確認を終えると、その後はあまり起動しないソフトになってしまいました。
色選択の機能も備えてはいますが、立体構造を立体のまま断面化するため、正直使いにくいのです。
そんな経緯で、「色選択」に主眼を置いたソフトウェアはどうあるべきか、が次の思索テーマとなりました。
市販のレイアウトツールや、色の指定を必要とするソフトには、必ず「色を選択」のパレットが備わっています。
共通して言えるのは、立体構造の色配列を何らかの工夫で平面化しているということです。
コンピューターのスクリーンは平面ですから、立体をそのまま扱うと操作がしにくくなるためでしょう。
例えば、Windows標準の色選択ダイアログは以下の様なものです。
[標準]タブ [ユーザー設定]タブ
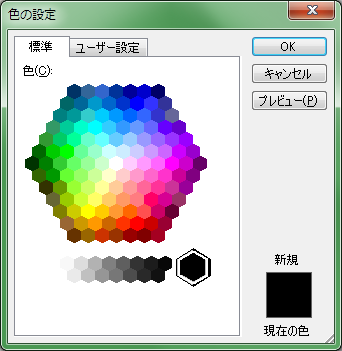
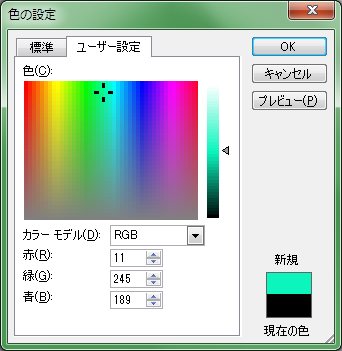 [標準]タブの平面図は、色相を循環させていますが、明度と彩度の規則性を犠牲にしています。
[ユーザー設定]タブの平面図は、明度と彩度の規則性を尊重していますが、
循環特性のある色相を赤の部分で分断しています。
もっとロジカルな均整を持ち、なおかつ実用的な「色の選択」モデルはないものでしょうか?
まず、色の3要素(色相・明度・彩度)のどれか1つを固定化することで立体を平面化することを考えました。
この場合、3つの平面図が考えられます。
(1)色相を固定化して、XY座標で明度と彩度を展開する。
(2)明度を固定化して、XY座標で彩度と色相を展開する。
(3)彩度を固定化して、XY座標で色相と明度を展開する。
ちなみに、Windows標準の色選択ダイアログの[ユーザー設定]タブは上記(2)のタイプに属し、
固定化している明度値は右側にある縦長の白黒バーで変更できるようになっています。
しかし白黒バーで調整しても平面図上の色は変化せず、右下の[新規]の欄が変化するだけです。
様々な検討を施しました。
その過程で、1つの平面ではなく2つを組み合わせて立体情報を与えた方が良いことに気づきました。
(3)の平面図は彩度の極限で“色”情報そのものが無くなってしまい無駄が多いパターンです。
そこで「色の立方体」をベースにし、(1)と(2)の2平面を連動させた「色の選択」モデルを考えてみました。
[標準]タブの平面図は、色相を循環させていますが、明度と彩度の規則性を犠牲にしています。
[ユーザー設定]タブの平面図は、明度と彩度の規則性を尊重していますが、
循環特性のある色相を赤の部分で分断しています。
もっとロジカルな均整を持ち、なおかつ実用的な「色の選択」モデルはないものでしょうか?
まず、色の3要素(色相・明度・彩度)のどれか1つを固定化することで立体を平面化することを考えました。
この場合、3つの平面図が考えられます。
(1)色相を固定化して、XY座標で明度と彩度を展開する。
(2)明度を固定化して、XY座標で彩度と色相を展開する。
(3)彩度を固定化して、XY座標で色相と明度を展開する。
ちなみに、Windows標準の色選択ダイアログの[ユーザー設定]タブは上記(2)のタイプに属し、
固定化している明度値は右側にある縦長の白黒バーで変更できるようになっています。
しかし白黒バーで調整しても平面図上の色は変化せず、右下の[新規]の欄が変化するだけです。
様々な検討を施しました。
その過程で、1つの平面ではなく2つを組み合わせて立体情報を与えた方が良いことに気づきました。
(3)の平面図は彩度の極限で“色”情報そのものが無くなってしまい無駄が多いパターンです。
そこで「色の立方体」をベースにし、(1)と(2)の2平面を連動させた「色の選択」モデルを考えてみました。
色の立方体を、頂点が白、底点が黒になるように配置することがこのモデルの出発点です。
このモデルを、白と黒を除く6つの頂点、すなわちR(赤)、G(緑)、B(青)、C(空)、M(紫)、Y(黄)が、
同一水平面になるように変形します。すると中央に正六角形が形成され、結果として2つの六角錘を
互いの底面で張り合わせた形状となります。これは以下の様な「双六角錐」(十二面体)となります。
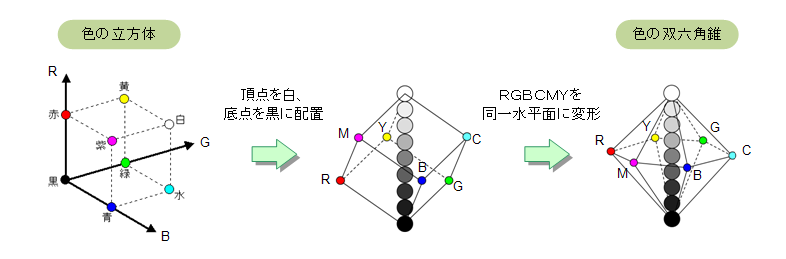 この立体モデルを2種類の断面で表現します。
この立体モデルを2種類の断面で表現します。
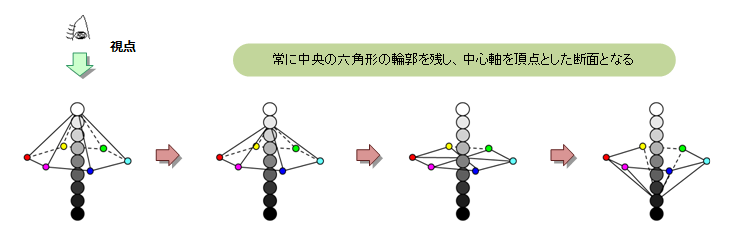
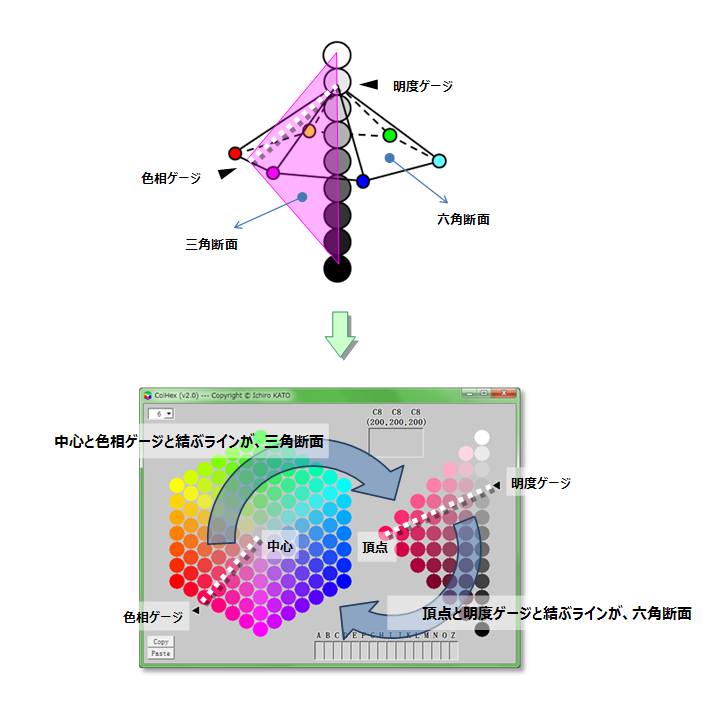
『 六角断面 』
1つ目の断面は、真上から観察するタイプです。
ただし、その断面は水平に切られるのではなく、常に中央の六角形の輪郭を残し、
白と黒を結ぶ中心軸上の任意の一点を含むように切断された面です。
この断面を、ここでは「六角断面」と呼びます。
六角形の外周は常にRGBCMYを含み、最大彩度になっています。そして中心の無彩色に向うにつれ、
各色相は次第にくすみ、彩度が落ちていきます。明度に関しては、この中心の無彩色の明度に応じて、
上がる場合もあれば下がる場合もあります。断面中心軸を上部から下部に向かって変化させると、
六角断面の中央の色は白から黒に変化し、全体の色調は次第に暗くなっていきます。よってこの断面は、
(2)の「明度を固定化して、XY座標で彩度と色相を展開する」タイプの変形版といえます。
この様に六角断面は、全色相の彩度と明度が中心の無彩色に向かって変化する様子を一望できることが特徴です。
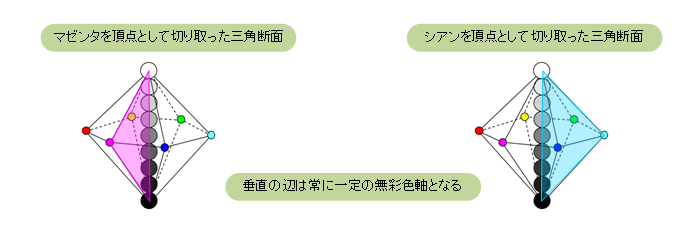
『 三角断面 』
2つ目の断面は、真横から観察するタイプであり、
双六角錐の任意の色相位置から中心軸に向かって垂直に切り取った断面です。
この断面を、ここでは「三角断面」と呼びます。
三角断面の垂直な辺は双六角錐の中心軸に相当し、どの断面においても常に一定です。
この辺は白から黒に向かう無彩色の軸となります。一方、無彩色軸と向かい合う頂点は、
双六角錐の中央六角形のいずれかの外周色になります。
よってこの断面は、(1)の「色相を固定化して、XY座標で明度と彩度を展開する」タイプそのものです。
三角断面は1つの色相に対する明度と彩度のグラデーションを一望できることが特徴です。
これら2つの断面(六角断面と三角断面)を並べて表示し、それを連動させたフリーソフトを開発しました。
そして、「ColHex(カラーヘキサ)」と名付けました。
それぞれの断面には、相手の断面位置を示す「ゲージ」が付いていており、
これを移動させることで、双六角錘の全体の色をスキャンすることができるという仕掛けです。
 ColHex(カラーヘキサ)をダウンロードします
ColHex(カラーヘキサ)をダウンロードします
 どうやらこの双六角錐モデルは「HLSモデル」という名称の既知モデルだったことを後日知りました。
しかし“色の立体モデルを扱うための表現断面”という命題に対しては、
これまでに無かった解を与えているのではないか、と自負しております。
どうやらこの双六角錐モデルは「HLSモデル」という名称の既知モデルだったことを後日知りました。
しかし“色の立体モデルを扱うための表現断面”という命題に対しては、
これまでに無かった解を与えているのではないか、と自負しております。
表紙に戻る
 ちなみにニュートンは、このスペクトルが7色よりなると主張しましたが、それは彼が音楽理論
との関係を意識したのだと言われています。彼は音程と色とを結びつけたかったのかもしれません。
ニュートンは、ピタゴラスやプラトンのように「神の調和」を強く意識する人物だったようです。
1936年にサザビーズのオークションにかけられたニュートンの秘密メモの中には、意外にも「錬金術」
に関するくだりがびっしり書かれているものがあったそうです。近代科学の扉を開けた天才ニュートン
も、まだ神秘的な時代の空気の中で生きていたのだ、ということを思い知らされる話です。
さて、20世紀に入ると色彩を体系的に把握する研究が起りました。
画家のマンセルが考案した色立体モデル(1905年)は、現代でもインテリアなどに利用され
ているシステムです。明度を上下に取り、白を頂点に黒を底点に配置します。その軸を
中心に色相で取囲み、彩度が上がるにつれて周辺に広げていきます。
心理的な色相をベースに構築されているため、全体の構造がデコボコしています。(左図)
真上から見ると、色相環と呼ばれる心理色相のリングが見られます。(右図)
これは、物理学的には1次元に並べられる周波数の対応色を、心理学的に輪状に組立て
直したと言えます。ちょっぴりゲーテの主張が感じられます。
ちなみにニュートンは、このスペクトルが7色よりなると主張しましたが、それは彼が音楽理論
との関係を意識したのだと言われています。彼は音程と色とを結びつけたかったのかもしれません。
ニュートンは、ピタゴラスやプラトンのように「神の調和」を強く意識する人物だったようです。
1936年にサザビーズのオークションにかけられたニュートンの秘密メモの中には、意外にも「錬金術」
に関するくだりがびっしり書かれているものがあったそうです。近代科学の扉を開けた天才ニュートン
も、まだ神秘的な時代の空気の中で生きていたのだ、ということを思い知らされる話です。
さて、20世紀に入ると色彩を体系的に把握する研究が起りました。
画家のマンセルが考案した色立体モデル(1905年)は、現代でもインテリアなどに利用され
ているシステムです。明度を上下に取り、白を頂点に黒を底点に配置します。その軸を
中心に色相で取囲み、彩度が上がるにつれて周辺に広げていきます。
心理的な色相をベースに構築されているため、全体の構造がデコボコしています。(左図)
真上から見ると、色相環と呼ばれる心理色相のリングが見られます。(右図)
これは、物理学的には1次元に並べられる周波数の対応色を、心理学的に輪状に組立て
直したと言えます。ちょっぴりゲーテの主張が感じられます。




 人間には、ある特定の波長の光に反応する細胞が3種類あり、
それがちょうど赤・緑・青の3つの色で表現される光で鋭い
感度ピークを示します。
この3つの波長(赤緑青)以外の光が視神経にあたると、複数
の細胞が適当な比率で刺激されるため、その案配で私たちは
色を識別しているわけです。
神の存在を信じたくなるような凄いシステムです。
それにしても、何故“3”なのでしょう? 内耳に存在する
三半規管は、空間が3次元であるという根拠があるにしても、
そもそも空間自体が“3”つの方向を持っている。
遺伝子情報の最小単位トリプレットも“3”です。
素粒子バリオンにおける構成クォークも3つ。
神様は、よほど“3”という数字がお好きなようです。(笑)
人間には、ある特定の波長の光に反応する細胞が3種類あり、
それがちょうど赤・緑・青の3つの色で表現される光で鋭い
感度ピークを示します。
この3つの波長(赤緑青)以外の光が視神経にあたると、複数
の細胞が適当な比率で刺激されるため、その案配で私たちは
色を識別しているわけです。
神の存在を信じたくなるような凄いシステムです。
それにしても、何故“3”なのでしょう? 内耳に存在する
三半規管は、空間が3次元であるという根拠があるにしても、
そもそも空間自体が“3”つの方向を持っている。
遺伝子情報の最小単位トリプレットも“3”です。
素粒子バリオンにおける構成クォークも3つ。
神様は、よほど“3”という数字がお好きなようです。(笑) さて、ここまでは先人達が築き上げた既知の発見や発案です。
私は一介の凡人にすぎませんが、恐れながら、私も少々色についての“思索”を行いましたので、
ここでご披露することにします。もちろん、すでに当然のように発見されていることで、私がそれ
を知らないだけかもしれませんが、私自身の“思索”でたどり着いたお話であることは神に誓います。
・・・と、大袈裟な前置をしましたが、大した発見ではありません。(笑)
マンセルの色立体モデルを中学の美術の教科書で知った私は、その何やら歪(いびつ)な形状に
一種の不満を感じました。色の体系は何故このようにデコボコしているんだろう? 本当は、
もっと美しいモデルが存在しているのではないだろうか?(その当時私はオストワルドのモデル
を知りませんでした)そのような気持を胸に抱きつつ月日が経ち、私はコンピューターに接する
ようになりました。そこで、光の三原色というものをグラフィック・プログラミングという世界
を通じて体験することになります。ご存知のようにコンピューターの世界での色表現は、RGB
の組合せで行います。私は、このRGBの規格性をもっと前面に押出したモデルが作れるのでは
ないかと考えたのです。
さて、ここまでは先人達が築き上げた既知の発見や発案です。
私は一介の凡人にすぎませんが、恐れながら、私も少々色についての“思索”を行いましたので、
ここでご披露することにします。もちろん、すでに当然のように発見されていることで、私がそれ
を知らないだけかもしれませんが、私自身の“思索”でたどり着いたお話であることは神に誓います。
・・・と、大袈裟な前置をしましたが、大した発見ではありません。(笑)
マンセルの色立体モデルを中学の美術の教科書で知った私は、その何やら歪(いびつ)な形状に
一種の不満を感じました。色の体系は何故このようにデコボコしているんだろう? 本当は、
もっと美しいモデルが存在しているのではないだろうか?(その当時私はオストワルドのモデル
を知りませんでした)そのような気持を胸に抱きつつ月日が経ち、私はコンピューターに接する
ようになりました。そこで、光の三原色というものをグラフィック・プログラミングという世界
を通じて体験することになります。ご存知のようにコンピューターの世界での色表現は、RGB
の組合せで行います。私は、このRGBの規格性をもっと前面に押出したモデルが作れるのでは
ないかと考えたのです。
 コンピュータの色指定はRGBの各輝度を指定し、
それを組合わせることで実現します。従って、
左図のようにR・G・Bの各輝度を各軸とした
3次元空間を設定すれば、すべての色がその座標
上にプロットされる事になります。しかも、輝度
は最大値を持っていますから空間内を無限に広が
るわけでなく、プロットされる領域は限定され、
それは立方体を形成します。
驚くべき事に、この立方体の中に世の中のすべて
の色が凝縮されていることになります。
コンピュータの色指定はRGBの各輝度を指定し、
それを組合わせることで実現します。従って、
左図のようにR・G・Bの各輝度を各軸とした
3次元空間を設定すれば、すべての色がその座標
上にプロットされる事になります。しかも、輝度
は最大値を持っていますから空間内を無限に広が
るわけでなく、プロットされる領域は限定され、
それは立方体を形成します。
驚くべき事に、この立方体の中に世の中のすべて
の色が凝縮されていることになります。 無彩色の中心軸と垂直に交わる平面で徐々にこの「色の立方体」を切っていくと、
3つの領域に分類されることがわかります。1つは白を頂点とした三角錐のエリアで、
この断面は正三角形を形成します。逆に黒を頂点とした三角錐のエリアが底側に存在します。
そしてその間には、断面が六角形となるエリアが存在しています。
以上が私の考えた「色の立方体」モデルです。
結果としては、あまりにも単純で誰にでも考え付きそうなものかもしれませんね。(笑)
しかし、ホームページやプログラミングでRGB指定に慣れ親しんでいても、これを
立体モデルとして把握するのは、ちょっとした思考の飛躍が必要だと思います。
事実、私もこのモデルを思い付いたのはRGBの制御を知って後、かなり経ってから
のことでした。このモデルを思い付いた時は、そのシンプルさが逆に嬉しかったのを
覚えています。
無彩色の中心軸と垂直に交わる平面で徐々にこの「色の立方体」を切っていくと、
3つの領域に分類されることがわかります。1つは白を頂点とした三角錐のエリアで、
この断面は正三角形を形成します。逆に黒を頂点とした三角錐のエリアが底側に存在します。
そしてその間には、断面が六角形となるエリアが存在しています。
以上が私の考えた「色の立方体」モデルです。
結果としては、あまりにも単純で誰にでも考え付きそうなものかもしれませんね。(笑)
しかし、ホームページやプログラミングでRGB指定に慣れ親しんでいても、これを
立体モデルとして把握するのは、ちょっとした思考の飛躍が必要だと思います。
事実、私もこのモデルを思い付いたのはRGBの制御を知って後、かなり経ってから
のことでした。このモデルを思い付いた時は、そのシンプルさが逆に嬉しかったのを
覚えています。

 そして、この2つの現象は以下の理由から生じるのではないかという1つの仮説を
立ててみました。両方とも同じ原因で起る現象と考えたのです。
そして、この2つの現象は以下の理由から生じるのではないかという1つの仮説を
立ててみました。両方とも同じ原因で起る現象と考えたのです。
 実際の曲線は、2次曲線なのか、3次曲線なのか、はたまたn次曲線なのか、
小数による次数の曲線なのか、それとも指数曲線なのか、あるいは非線形曲線なのか、
それは実際の測定でないと決定できませんが、とりあえず最もシンプルな2次曲線で
補正してみました。結果は以下のとおりです。
実際の曲線は、2次曲線なのか、3次曲線なのか、はたまたn次曲線なのか、
小数による次数の曲線なのか、それとも指数曲線なのか、あるいは非線形曲線なのか、
それは実際の測定でないと決定できませんが、とりあえず最もシンプルな2次曲線で
補正してみました。結果は以下のとおりです。
 この結果を眺めると、なかなか良い具合に補正できているようです。
実際には、R・G・Bの各輝度の補正曲線の特性は、それぞれの視覚細胞によって
微妙に異なることでしょう。もし測定実験によりそれらの補正曲線が明確になれば、
「色の立方体」モデルは、その結果を容易に組込むことが出来ます。人間の持つ視覚
細胞と対応した生物学的補正が一意に行えるモデルなのです。
「色の立方体」モデル。それはとても単純で、しかもRGB値を並べただけという
極めて機械的なものです。しかし輝度補正を加えることで、物理的解釈と生理的解釈
がバランスした面白いモデルになったと思っています。
この結果を眺めると、なかなか良い具合に補正できているようです。
実際には、R・G・Bの各輝度の補正曲線の特性は、それぞれの視覚細胞によって
微妙に異なることでしょう。もし測定実験によりそれらの補正曲線が明確になれば、
「色の立方体」モデルは、その結果を容易に組込むことが出来ます。人間の持つ視覚
細胞と対応した生物学的補正が一意に行えるモデルなのです。
「色の立方体」モデル。それはとても単純で、しかもRGB値を並べただけという
極めて機械的なものです。しかし輝度補正を加えることで、物理的解釈と生理的解釈
がバランスした面白いモデルになったと思っています。

 [標準]タブの平面図は、色相を循環させていますが、明度と彩度の規則性を犠牲にしています。
[ユーザー設定]タブの平面図は、明度と彩度の規則性を尊重していますが、
循環特性のある色相を赤の部分で分断しています。
もっとロジカルな均整を持ち、なおかつ実用的な「色の選択」モデルはないものでしょうか?
まず、色の3要素(色相・明度・彩度)のどれか1つを固定化することで立体を平面化することを考えました。
この場合、3つの平面図が考えられます。
(1)色相を固定化して、XY座標で明度と彩度を展開する。
(2)明度を固定化して、XY座標で彩度と色相を展開する。
(3)彩度を固定化して、XY座標で色相と明度を展開する。
ちなみに、Windows標準の色選択ダイアログの[ユーザー設定]タブは上記(2)のタイプに属し、
固定化している明度値は右側にある縦長の白黒バーで変更できるようになっています。
しかし白黒バーで調整しても平面図上の色は変化せず、右下の[新規]の欄が変化するだけです。
様々な検討を施しました。
その過程で、1つの平面ではなく2つを組み合わせて立体情報を与えた方が良いことに気づきました。
(3)の平面図は彩度の極限で“色”情報そのものが無くなってしまい無駄が多いパターンです。
そこで「色の立方体」をベースにし、(1)と(2)の2平面を連動させた「色の選択」モデルを考えてみました。
[標準]タブの平面図は、色相を循環させていますが、明度と彩度の規則性を犠牲にしています。
[ユーザー設定]タブの平面図は、明度と彩度の規則性を尊重していますが、
循環特性のある色相を赤の部分で分断しています。
もっとロジカルな均整を持ち、なおかつ実用的な「色の選択」モデルはないものでしょうか?
まず、色の3要素(色相・明度・彩度)のどれか1つを固定化することで立体を平面化することを考えました。
この場合、3つの平面図が考えられます。
(1)色相を固定化して、XY座標で明度と彩度を展開する。
(2)明度を固定化して、XY座標で彩度と色相を展開する。
(3)彩度を固定化して、XY座標で色相と明度を展開する。
ちなみに、Windows標準の色選択ダイアログの[ユーザー設定]タブは上記(2)のタイプに属し、
固定化している明度値は右側にある縦長の白黒バーで変更できるようになっています。
しかし白黒バーで調整しても平面図上の色は変化せず、右下の[新規]の欄が変化するだけです。
様々な検討を施しました。
その過程で、1つの平面ではなく2つを組み合わせて立体情報を与えた方が良いことに気づきました。
(3)の平面図は彩度の極限で“色”情報そのものが無くなってしまい無駄が多いパターンです。
そこで「色の立方体」をベースにし、(1)と(2)の2平面を連動させた「色の選択」モデルを考えてみました。
 この立体モデルを2種類の断面で表現します。
この立体モデルを2種類の断面で表現します。


 どうやらこの双六角錐モデルは「HLSモデル」という名称の既知モデルだったことを後日知りました。
しかし“色の立体モデルを扱うための表現断面”という命題に対しては、
これまでに無かった解を与えているのではないか、と自負しております。
どうやらこの双六角錐モデルは「HLSモデル」という名称の既知モデルだったことを後日知りました。
しかし“色の立体モデルを扱うための表現断面”という命題に対しては、
これまでに無かった解を与えているのではないか、と自負しております。