表紙に戻る
デカウス空間
私が高校時代に使用した(使用させられた)数学の教科書は、東京書籍のものでした。
その教科書には、各章の中表紙にとても小粋な文章が書いてありました。
例えば「三章:平面図形と式」の冒頭は次のような記述でした。
|
デカルト(1596~1650)による代数と幾何学の美しい融合は、
今日もデカルト座標の名を残している。点を座標によって
表せば、図形の間の諸関係が式で表示され、幾何学的発見
と代数的発見とは一体化する。18世紀にそれは絢爛と開
花したが、この強力な思想は現代数学のなかでもいまだに
発展しつつある。
|
私はこの文章の意味を、後日授業の中で感動を持って知ることになります。
それは、二次方程式の解が、座標平面内の放物線とX軸の交点で表される
という事実でした。その時の驚愕を未だに忘れることができません。
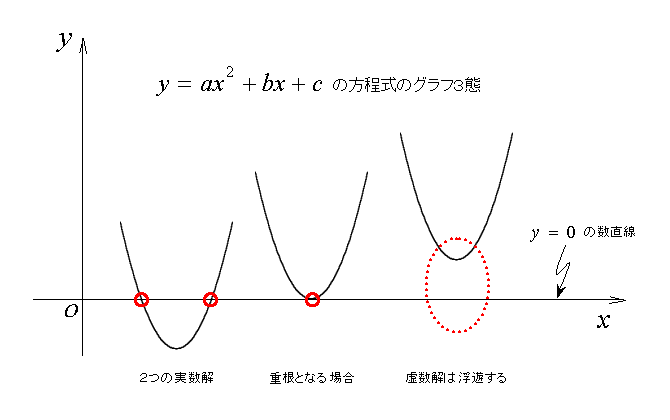 二次方程式の解が重根となるとき、放物線の頂点がX軸と接する。
「なんて直感的で美しいのだろう!」
私はすっかりデカルト平面の虜になってしまいました。
どんな方程式もこの平面内に視覚的に表現できるのです。
そして、その解をX軸との交点として確認することができるのです。
虚数解に至っては、X軸と接することなく放物線は浮遊します。
このことも、私にはとても魅力的に感じました。
デカルト平面にとって、X軸は実数の世界の数直線です。
ここに交点が現れるはずはありません。
実に理に叶っているではありませんか!
数学が本当に得意な方は、逆にこの程度のことで一々感銘を受けないかもしれません。
しかし幸いなことに、私はデカルト平面で感動できる程度の学力でした。(笑)
その後、数学の授業は淡々と進み、新しい単元にどんどん移っていきました。
そんなある日、数学の先生があるプリントを配ったのです。それは、高校数学の
テリトリーを逸脱したものでした。しかし、その先生が「これは余談だけどね」と
言いながら配布したそのプリントがなければ、私はこれからご説明する発見を
しなかったかもしれません。
そのプリントにはガウス平面の説明が書かれていました。
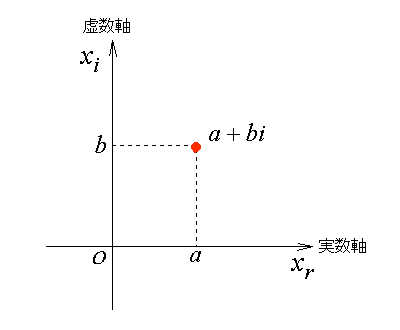
ガウス平面はX軸を実数軸としY軸を虚数軸として、すべての複素数を
その平面上のプロット(点)で表現できます。つまり、数学上のあらゆる「数」が、
この平面内で表現できるわけです。この平面も私を魅了するに充分でした。
二次方程式の解が重根となるとき、放物線の頂点がX軸と接する。
「なんて直感的で美しいのだろう!」
私はすっかりデカルト平面の虜になってしまいました。
どんな方程式もこの平面内に視覚的に表現できるのです。
そして、その解をX軸との交点として確認することができるのです。
虚数解に至っては、X軸と接することなく放物線は浮遊します。
このことも、私にはとても魅力的に感じました。
デカルト平面にとって、X軸は実数の世界の数直線です。
ここに交点が現れるはずはありません。
実に理に叶っているではありませんか!
数学が本当に得意な方は、逆にこの程度のことで一々感銘を受けないかもしれません。
しかし幸いなことに、私はデカルト平面で感動できる程度の学力でした。(笑)
その後、数学の授業は淡々と進み、新しい単元にどんどん移っていきました。
そんなある日、数学の先生があるプリントを配ったのです。それは、高校数学の
テリトリーを逸脱したものでした。しかし、その先生が「これは余談だけどね」と
言いながら配布したそのプリントがなければ、私はこれからご説明する発見を
しなかったかもしれません。
そのプリントにはガウス平面の説明が書かれていました。
ガウス平面はX軸を実数軸としY軸を虚数軸として、すべての複素数を
その平面上のプロット(点)で表現できます。つまり、数学上のあらゆる「数」が、
この平面内で表現できるわけです。この平面も私を魅了するに充分でした。
 その時、私の頭の中でデカルト平面とガウス平面が融合したのです!
どうしてそれがひらめいたのか、自分でも分りません。
しかしそれは三次元空間として、私の頭の中で鮮明にイメージされました。
その時、私の頭の中でデカルト平面とガウス平面が融合したのです!
どうしてそれがひらめいたのか、自分でも分りません。
しかしそれは三次元空間として、私の頭の中で鮮明にイメージされました。
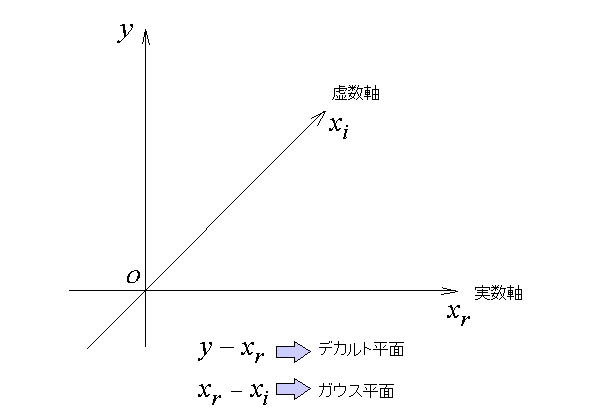 次に私が考えたのは、この空間の中にあの「感動の放物線」を描いたら何が起るか
という事でした。もしかしたら、二次方程式の解が、たとえ虚数解であっても、
この空間の中にプロットされるかもしれない。いや、プロットされるはずだ。
そのプロットをトレースしたら、「本当の放物線」の姿が見えてくるかもしれない!
私はもう夢中でした。そして、とてつもなく美しい放物線の軌跡を発見したのです。
次に私が考えたのは、この空間の中にあの「感動の放物線」を描いたら何が起るか
という事でした。もしかしたら、二次方程式の解が、たとえ虚数解であっても、
この空間の中にプロットされるかもしれない。いや、プロットされるはずだ。
そのプロットをトレースしたら、「本当の放物線」の姿が見えてくるかもしれない!
私はもう夢中でした。そして、とてつもなく美しい放物線の軌跡を発見したのです。
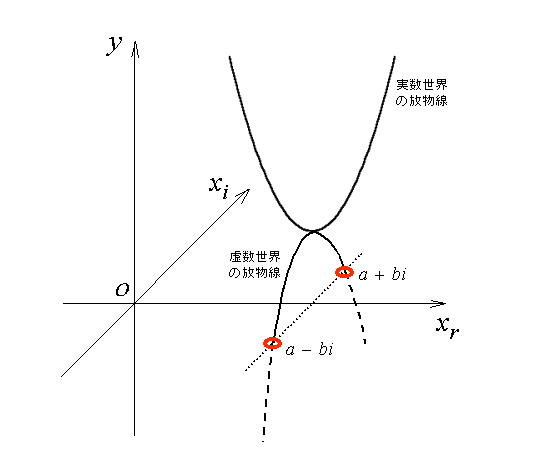 二次方程式が描く放物線。
教科書や参考書に載っているそれは、実はその一部でしかなく、
デカルト平面では描画できない、もう一つ別の影のような軌跡が存在していたのです。
それは、三次元空間の中で初めて姿を現す虚数世界の曲線です。
その虚数の放物線は、実数の放物線と頂点で接し、それぞれが属する平面は直角に
交わっています。そして、互いの放物線の開き具合は等しいのです!
二次方程式の複素数解が、互いに共役の関係にあることも視覚的に把握できます。
虚数解の実数要素が、その放物線の重根(頂点)に等しいことも一目瞭然です。
私は早速、この空間に名前を付けようと考えました。
デカルト平面とガウス平面を融合し出来上った空間ですから、
デカルト+ガウス=デカウスと名付けることにしました。
“でっかい臼”みたいで滑稽かもしれませんが、それなりに韻を踏んでいて気に入っています。
巨匠デカルトも天才ガウスも、笑って許してくれることでしょう。
こうして「デカウス空間」ができあがりました。
デカルト平面では、その方程式の解はX軸という1次元の線との交点で
表現されていました。しかしデカウス空間では、Xr軸とXi軸で構成される
2次平面との交点で表現されます。この平面はガウス平面ですから、
複素数というすべての数を視覚化できることになります。
では、3次曲線はどんな姿を見せてくれるのだろう?
4次曲線は? 双曲線はどうだろう? 円や楕円は!?
更には、対数曲線や三角関数はどうなんだろう?
私の頭の中は爆発しそうでした。
それらの姿を描き出す作業は、まるで実験物理学者のようでした。
与えられた方程式の定数項を少しずつ変化させることで、
Y軸に沿った平行移動を行い、それらの虚数解を算出しプロットしていくのです。
今のようにパソコンも無いし、関数電卓も普及していなかったので大変でした。
数学を専攻している人なら、空間内の虚曲線を表現する代数的アプローチが出来た
でしょうが、高校生の私には、上記のような手作業で虚曲線を描くことが精一杯でした。
しかし、その作業は驚きと発見の連続であり、全く苦になりませんでした。
今も手元に、その当時書散らしたメモが残っています。
私は、まずn次方程式の基本形 y = xn から考察しました。
これは比較的簡単で、しかもシンメトリックな美しい形状が浮び上がってきました。
二次方程式が描く放物線。
教科書や参考書に載っているそれは、実はその一部でしかなく、
デカルト平面では描画できない、もう一つ別の影のような軌跡が存在していたのです。
それは、三次元空間の中で初めて姿を現す虚数世界の曲線です。
その虚数の放物線は、実数の放物線と頂点で接し、それぞれが属する平面は直角に
交わっています。そして、互いの放物線の開き具合は等しいのです!
二次方程式の複素数解が、互いに共役の関係にあることも視覚的に把握できます。
虚数解の実数要素が、その放物線の重根(頂点)に等しいことも一目瞭然です。
私は早速、この空間に名前を付けようと考えました。
デカルト平面とガウス平面を融合し出来上った空間ですから、
デカルト+ガウス=デカウスと名付けることにしました。
“でっかい臼”みたいで滑稽かもしれませんが、それなりに韻を踏んでいて気に入っています。
巨匠デカルトも天才ガウスも、笑って許してくれることでしょう。
こうして「デカウス空間」ができあがりました。
デカルト平面では、その方程式の解はX軸という1次元の線との交点で
表現されていました。しかしデカウス空間では、Xr軸とXi軸で構成される
2次平面との交点で表現されます。この平面はガウス平面ですから、
複素数というすべての数を視覚化できることになります。
では、3次曲線はどんな姿を見せてくれるのだろう?
4次曲線は? 双曲線はどうだろう? 円や楕円は!?
更には、対数曲線や三角関数はどうなんだろう?
私の頭の中は爆発しそうでした。
それらの姿を描き出す作業は、まるで実験物理学者のようでした。
与えられた方程式の定数項を少しずつ変化させることで、
Y軸に沿った平行移動を行い、それらの虚数解を算出しプロットしていくのです。
今のようにパソコンも無いし、関数電卓も普及していなかったので大変でした。
数学を専攻している人なら、空間内の虚曲線を表現する代数的アプローチが出来た
でしょうが、高校生の私には、上記のような手作業で虚曲線を描くことが精一杯でした。
しかし、その作業は驚きと発見の連続であり、全く苦になりませんでした。
今も手元に、その当時書散らしたメモが残っています。
私は、まずn次方程式の基本形 y = xn から考察しました。
これは比較的簡単で、しかもシンメトリックな美しい形状が浮び上がってきました。
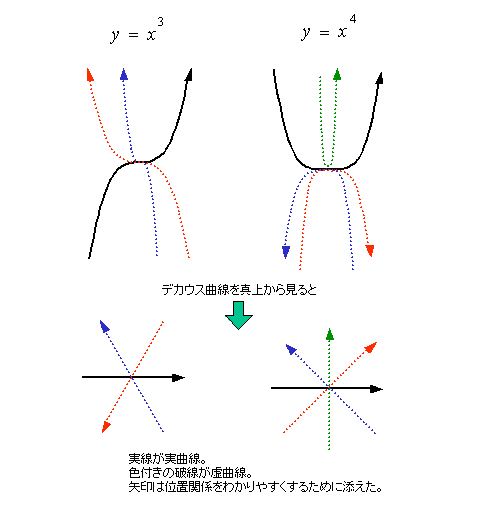 基本形n次方程式の実曲線に虚曲線を加えると、見事な均等配置となります。
それらを真上から見ると、まるでケーキを公平に2n分割するような線となっています。
奇数次の方程式の場合は、ちょうど各曲線がその変曲点の部分ではすかいに交差し、
偶数次の方程式の場合は、極値点において π/n だけ回転して交わります。
なんて均整の取れた姿なのでしょう!
これが、n次方程式の本当の幾何学的姿だったのです。
さて、次は一般的なn次方程式です。
一般的なn次方程式は、極値点や変曲点を複雑に持っているため、
基本的なn次方程式のように簡単には描けません。
しかし、いくつかの原則が見えてきました。
以下の図が、一般的な3次方程式と4次方程式のデカウス曲線の形状です。
基本形n次方程式の実曲線に虚曲線を加えると、見事な均等配置となります。
それらを真上から見ると、まるでケーキを公平に2n分割するような線となっています。
奇数次の方程式の場合は、ちょうど各曲線がその変曲点の部分ではすかいに交差し、
偶数次の方程式の場合は、極値点において π/n だけ回転して交わります。
なんて均整の取れた姿なのでしょう!
これが、n次方程式の本当の幾何学的姿だったのです。
さて、次は一般的なn次方程式です。
一般的なn次方程式は、極値点や変曲点を複雑に持っているため、
基本的なn次方程式のように簡単には描けません。
しかし、いくつかの原則が見えてきました。
以下の図が、一般的な3次方程式と4次方程式のデカウス曲線の形状です。
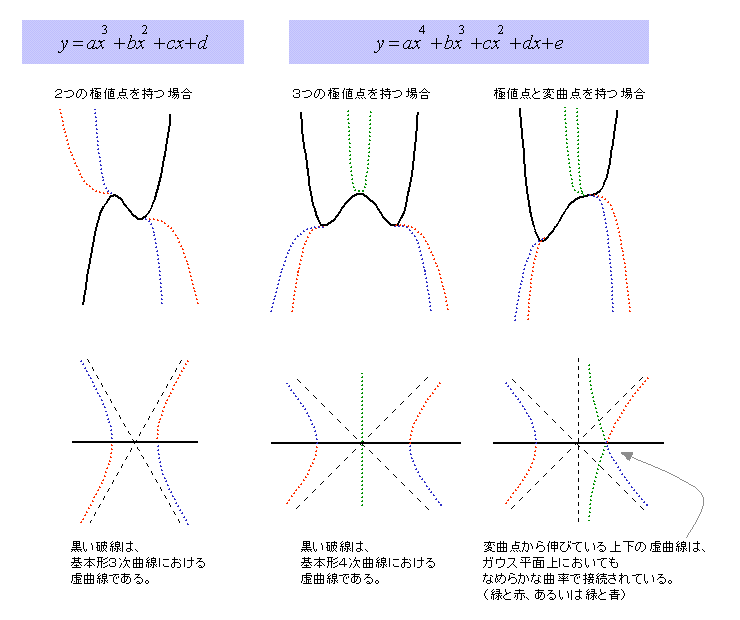
| (原則1) |
虚曲線は、実曲線の極値点・変曲点から分岐する。 |
| (原則2) |
どのようなn次方程式であっても、その虚曲線は基本形のn次方程式に
おける虚曲線に漸近する。このことは、n-1次以降の低次項により、
原点付近のデカウス曲線の形状が“乱されている”という解釈を可能とする。 |
| (原則3) |
n次方程式には“解の重心”が存在し、その値は定数項に寄らず一定である。 |
特に、(原則3)に関しては、とても興味深い発見をいくつかしました。
“解の重心”とは、私が勝手に命名したもので、ガウス平面上にプロットした複数の解を
相加平均して求められる値です。n次方程式の複素解は共役な対として出現しますから、
虚数項は打ち消し合い、解の重心は常に実数となります。
n次方程式の定数項を変化させると、デカウス曲線全体がy軸に沿って上下に移動する
ことになりますが、その際“解の重心”が保存されるというのが(原則3)です。
更に、解の重心はとても簡単に求めることが出来るのを発見しました。
n次方程式が与えられた場合、n次項の係数をa、n-1次項の係数をbとすると、
解の重心 = -b/(a×n)
となります。実は、この関係式は、初めはもっと複雑な手続で得られると考えていました。
「n次方程式の解の重心を求めるには、その方程式をn-1回連続して微分し、
そこで得られた1次方程式を解くことで得られる」
というものでした。私がこの手続をどの様にして発見したか、それを説明することは
自分でも出来ません。まったくの閃きだったのです。
さて、3次方程式や4次方程式の解を求める手法を見てみると、必ずn-1次の項を
消去することから始めています。そして、その方法はxを
x = t - b/(a×n)
と置換することで行っています。つまりデカウス幾何学的に解釈すると、デカウス曲線の
解の重心をx=0の原点にシフトするという操作を行っていることになります。
これらの発見も、私には実に興味深いことに感じました。
このデカウス空間に対する探索を行っている過程で、5次方程式の代数的解法が
存在せず、そのことをガロアが自ら創設した群論によって証明したことなども知りました。
確かに、5次方程式以上の“代数的”解法は存在しないかもしれません。
しかし、このデカウス空間内の虚曲線の性質を突詰めていくと、もしかしたら
三角関数や対数関数、双曲線関数などの関数を使って、
一般的なn次方程式の解を表現できるかもしれない、と思っています。
それは、素人的な発想かもしれませんが、実に愉快でワクワクする想像です。
デカウス空間による代数と幾何学の新しい融合。私はこの発見をどうにかして
世の中に伝えたいと考えました。しかし、この発見が学会や専門誌への投稿に耐えうる
レベルでないことも自覚していました。だからせいぜい、数学に興味があるという人や
数学を専攻していたという人に出会うたびに、口頭で説明し続けるに留めていたのです。
加藤という名は残らなくても、もしかしたら口伝えで伝承され、何らかの形で人類史に
貢献できるかもしれないと考えていました。
(全く大袈裟ですが、私はゼロを発見した無名のインド人をイメージしていたのです)
今日、インターネットという個人から全世界への公開手段を得て、
私はここにデカウス空間の発見を発信できる喜びを感じています。
冷静に考えると、デカウス空間は一つの表現法に過ぎず、
これが数学的発見かというと、ちょっと言過ぎかもしれません。
また、私の専門は数学ではないのでこの発見を次に進める術も知りません。
ただ一つ言えるのは、浮遊する放物線の虚数解をデカウス空間内にプロット
できた時の感動は、いまでも鮮明に覚えているということです。
それは、「本物の美」をかいま見た時におこる感動と同質のものでした。
●追記1
本ページ公開後、chunさんからデカウス空間を発展させるアイディアをメールで頂きました。
その作業自体をお願いしたところ、素晴しい内容のレポートを頂きました。
指数関数の虚曲線がらせん状にプロットされるのです!
しかも、Y軸側をガウス平面として作画する新しい切口の展開でした。
これは、デカウス空間の逆関数表現とも言えるかもしれません。
この空間を私は、chunさんへの敬意を込めて「デカマウス空間」と呼びたいです。(笑)
ここに、その素晴しいレポートを掲載いたします。
●追記2
後日、デカ(マ)ウス空間に刺激を受けたASAJIさんが、de Moivreの公式を縦横に駆使し、
「私の愛情は虚(うつろ)ではない」という真実を導きました。(笑)
●追記3
さらにchunさんが、上記の“真実”を導出する過程から、
虚数の指数関数におけるデカウス空間の姿に到達。
そのレポートをメールで送ってきてくれました。
このコラボレーション! たまらない感動です。
●追記4
chunさんのレポートに対し、今度はASAJIさんが
“複素数指数関数の一般デカマウス空間の分析”レポートを執筆してくれました。
シャンパングラスに美しく螺旋を描く画像まで付いています。
しかもその画像は、なんと! ご自身が作成されたソフトで出力したとのこと!
ダウンロードページとしてASAJIさんのHPへのリンクも張らせて頂きました。
●追記5
Cassiopeiaさんから、素晴しいメールを頂きました。
「等値線」による4次元空間の表現です。
色も活用し、見事な円の虚曲線が展開されています。
この井上雄介さんの着想、私は「超デカマウス空間」と名付けたいです。(笑)
●追記6
またまたCassiopeiaさんから、メールを頂きました。
今度は、「解の重心」に関するレポートです。
長年の私的仮説が、いとも簡単に証明されています。
ありがとうございました。
●追記7
Keiさんが授業で習った「オイラーの等式」を展開して、
デカウス空間に三角関数のデカウス曲線を描いてくれました。
私も試してみたかった命題です。
想像通りの素晴らしい曲線です。
波動のピークから周期的に延びる双曲線が実に美しい!
●追記8
双曲線のデカウス曲線に端を発し、
るうさんが超デカマウス空間を扱うソフトを開発しました。
通常では表現不可能な4次元構造を、色調を活用して表しています。
まったくもって素晴らしい発想と技術です。
このソフトがあると、超デカマウス空間の描像を得ることが出来ます。
これらの追記の詳細を見る
表紙に戻る
 二次方程式の解が重根となるとき、放物線の頂点がX軸と接する。
「なんて直感的で美しいのだろう!」
私はすっかりデカルト平面の虜になってしまいました。
どんな方程式もこの平面内に視覚的に表現できるのです。
そして、その解をX軸との交点として確認することができるのです。
虚数解に至っては、X軸と接することなく放物線は浮遊します。
このことも、私にはとても魅力的に感じました。
デカルト平面にとって、X軸は実数の世界の数直線です。
ここに交点が現れるはずはありません。
実に理に叶っているではありませんか!
数学が本当に得意な方は、逆にこの程度のことで一々感銘を受けないかもしれません。
しかし幸いなことに、私はデカルト平面で感動できる程度の学力でした。(笑)
その後、数学の授業は淡々と進み、新しい単元にどんどん移っていきました。
そんなある日、数学の先生があるプリントを配ったのです。それは、高校数学の
テリトリーを逸脱したものでした。しかし、その先生が「これは余談だけどね」と
言いながら配布したそのプリントがなければ、私はこれからご説明する発見を
しなかったかもしれません。
そのプリントにはガウス平面の説明が書かれていました。
ガウス平面はX軸を実数軸としY軸を虚数軸として、すべての複素数を
その平面上のプロット(点)で表現できます。つまり、数学上のあらゆる「数」が、
この平面内で表現できるわけです。この平面も私を魅了するに充分でした。
二次方程式の解が重根となるとき、放物線の頂点がX軸と接する。
「なんて直感的で美しいのだろう!」
私はすっかりデカルト平面の虜になってしまいました。
どんな方程式もこの平面内に視覚的に表現できるのです。
そして、その解をX軸との交点として確認することができるのです。
虚数解に至っては、X軸と接することなく放物線は浮遊します。
このことも、私にはとても魅力的に感じました。
デカルト平面にとって、X軸は実数の世界の数直線です。
ここに交点が現れるはずはありません。
実に理に叶っているではありませんか!
数学が本当に得意な方は、逆にこの程度のことで一々感銘を受けないかもしれません。
しかし幸いなことに、私はデカルト平面で感動できる程度の学力でした。(笑)
その後、数学の授業は淡々と進み、新しい単元にどんどん移っていきました。
そんなある日、数学の先生があるプリントを配ったのです。それは、高校数学の
テリトリーを逸脱したものでした。しかし、その先生が「これは余談だけどね」と
言いながら配布したそのプリントがなければ、私はこれからご説明する発見を
しなかったかもしれません。
そのプリントにはガウス平面の説明が書かれていました。
ガウス平面はX軸を実数軸としY軸を虚数軸として、すべての複素数を
その平面上のプロット(点)で表現できます。つまり、数学上のあらゆる「数」が、
この平面内で表現できるわけです。この平面も私を魅了するに充分でした。
 その時、私の頭の中でデカルト平面とガウス平面が融合したのです!
どうしてそれがひらめいたのか、自分でも分りません。
しかしそれは三次元空間として、私の頭の中で鮮明にイメージされました。
その時、私の頭の中でデカルト平面とガウス平面が融合したのです!
どうしてそれがひらめいたのか、自分でも分りません。
しかしそれは三次元空間として、私の頭の中で鮮明にイメージされました。
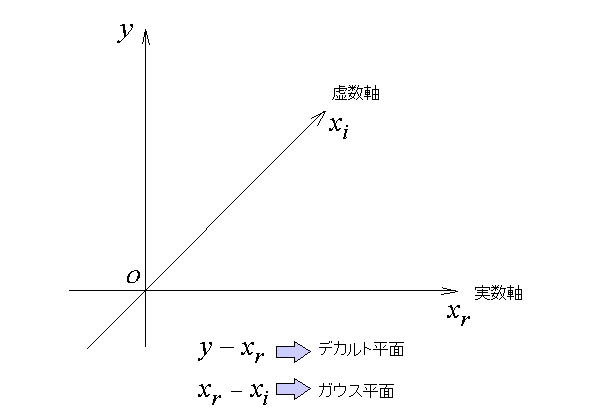 次に私が考えたのは、この空間の中にあの「感動の放物線」を描いたら何が起るか
という事でした。もしかしたら、二次方程式の解が、たとえ虚数解であっても、
この空間の中にプロットされるかもしれない。いや、プロットされるはずだ。
そのプロットをトレースしたら、「本当の放物線」の姿が見えてくるかもしれない!
私はもう夢中でした。そして、とてつもなく美しい放物線の軌跡を発見したのです。
次に私が考えたのは、この空間の中にあの「感動の放物線」を描いたら何が起るか
という事でした。もしかしたら、二次方程式の解が、たとえ虚数解であっても、
この空間の中にプロットされるかもしれない。いや、プロットされるはずだ。
そのプロットをトレースしたら、「本当の放物線」の姿が見えてくるかもしれない!
私はもう夢中でした。そして、とてつもなく美しい放物線の軌跡を発見したのです。
 二次方程式が描く放物線。
教科書や参考書に載っているそれは、実はその一部でしかなく、
デカルト平面では描画できない、もう一つ別の影のような軌跡が存在していたのです。
それは、三次元空間の中で初めて姿を現す虚数世界の曲線です。
その虚数の放物線は、実数の放物線と頂点で接し、それぞれが属する平面は直角に
交わっています。そして、互いの放物線の開き具合は等しいのです!
二次方程式の複素数解が、互いに共役の関係にあることも視覚的に把握できます。
虚数解の実数要素が、その放物線の重根(頂点)に等しいことも一目瞭然です。
私は早速、この空間に名前を付けようと考えました。
デカルト平面とガウス平面を融合し出来上った空間ですから、
デカルト+ガウス=デカウスと名付けることにしました。
“でっかい臼”みたいで滑稽かもしれませんが、それなりに韻を踏んでいて気に入っています。
巨匠デカルトも天才ガウスも、笑って許してくれることでしょう。
こうして「デカウス空間」ができあがりました。
デカルト平面では、その方程式の解はX軸という1次元の線との交点で
表現されていました。しかしデカウス空間では、Xr軸とXi軸で構成される
2次平面との交点で表現されます。この平面はガウス平面ですから、
複素数というすべての数を視覚化できることになります。
では、3次曲線はどんな姿を見せてくれるのだろう?
4次曲線は? 双曲線はどうだろう? 円や楕円は!?
更には、対数曲線や三角関数はどうなんだろう?
私の頭の中は爆発しそうでした。
それらの姿を描き出す作業は、まるで実験物理学者のようでした。
与えられた方程式の定数項を少しずつ変化させることで、
Y軸に沿った平行移動を行い、それらの虚数解を算出しプロットしていくのです。
今のようにパソコンも無いし、関数電卓も普及していなかったので大変でした。
数学を専攻している人なら、空間内の虚曲線を表現する代数的アプローチが出来た
でしょうが、高校生の私には、上記のような手作業で虚曲線を描くことが精一杯でした。
しかし、その作業は驚きと発見の連続であり、全く苦になりませんでした。
今も手元に、その当時書散らしたメモが残っています。
私は、まずn次方程式の基本形 y = xn から考察しました。
これは比較的簡単で、しかもシンメトリックな美しい形状が浮び上がってきました。
二次方程式が描く放物線。
教科書や参考書に載っているそれは、実はその一部でしかなく、
デカルト平面では描画できない、もう一つ別の影のような軌跡が存在していたのです。
それは、三次元空間の中で初めて姿を現す虚数世界の曲線です。
その虚数の放物線は、実数の放物線と頂点で接し、それぞれが属する平面は直角に
交わっています。そして、互いの放物線の開き具合は等しいのです!
二次方程式の複素数解が、互いに共役の関係にあることも視覚的に把握できます。
虚数解の実数要素が、その放物線の重根(頂点)に等しいことも一目瞭然です。
私は早速、この空間に名前を付けようと考えました。
デカルト平面とガウス平面を融合し出来上った空間ですから、
デカルト+ガウス=デカウスと名付けることにしました。
“でっかい臼”みたいで滑稽かもしれませんが、それなりに韻を踏んでいて気に入っています。
巨匠デカルトも天才ガウスも、笑って許してくれることでしょう。
こうして「デカウス空間」ができあがりました。
デカルト平面では、その方程式の解はX軸という1次元の線との交点で
表現されていました。しかしデカウス空間では、Xr軸とXi軸で構成される
2次平面との交点で表現されます。この平面はガウス平面ですから、
複素数というすべての数を視覚化できることになります。
では、3次曲線はどんな姿を見せてくれるのだろう?
4次曲線は? 双曲線はどうだろう? 円や楕円は!?
更には、対数曲線や三角関数はどうなんだろう?
私の頭の中は爆発しそうでした。
それらの姿を描き出す作業は、まるで実験物理学者のようでした。
与えられた方程式の定数項を少しずつ変化させることで、
Y軸に沿った平行移動を行い、それらの虚数解を算出しプロットしていくのです。
今のようにパソコンも無いし、関数電卓も普及していなかったので大変でした。
数学を専攻している人なら、空間内の虚曲線を表現する代数的アプローチが出来た
でしょうが、高校生の私には、上記のような手作業で虚曲線を描くことが精一杯でした。
しかし、その作業は驚きと発見の連続であり、全く苦になりませんでした。
今も手元に、その当時書散らしたメモが残っています。
私は、まずn次方程式の基本形 y = xn から考察しました。
これは比較的簡単で、しかもシンメトリックな美しい形状が浮び上がってきました。
 基本形n次方程式の実曲線に虚曲線を加えると、見事な均等配置となります。
それらを真上から見ると、まるでケーキを公平に2n分割するような線となっています。
奇数次の方程式の場合は、ちょうど各曲線がその変曲点の部分ではすかいに交差し、
偶数次の方程式の場合は、極値点において π/n だけ回転して交わります。
なんて均整の取れた姿なのでしょう!
これが、n次方程式の本当の幾何学的姿だったのです。
さて、次は一般的なn次方程式です。
一般的なn次方程式は、極値点や変曲点を複雑に持っているため、
基本的なn次方程式のように簡単には描けません。
しかし、いくつかの原則が見えてきました。
以下の図が、一般的な3次方程式と4次方程式のデカウス曲線の形状です。
基本形n次方程式の実曲線に虚曲線を加えると、見事な均等配置となります。
それらを真上から見ると、まるでケーキを公平に2n分割するような線となっています。
奇数次の方程式の場合は、ちょうど各曲線がその変曲点の部分ではすかいに交差し、
偶数次の方程式の場合は、極値点において π/n だけ回転して交わります。
なんて均整の取れた姿なのでしょう!
これが、n次方程式の本当の幾何学的姿だったのです。
さて、次は一般的なn次方程式です。
一般的なn次方程式は、極値点や変曲点を複雑に持っているため、
基本的なn次方程式のように簡単には描けません。
しかし、いくつかの原則が見えてきました。
以下の図が、一般的な3次方程式と4次方程式のデカウス曲線の形状です。
